Age (model theory)
Encyclopedia
In model theory
, the age of a structure
(or model) A is the class of all finitely generated structures which are embeddable
in A (i.e. isomorphic to substructures of A). This concept is central in the construction of a Fraïssé
limit.
The main point of Fraïssé's construction is to show how one can approximate a structure by its finitely generated substructures. Thus for example the age of any dense linear order without endpoints (DLO),
is precisely the set of all finite linear orderings, which are distinguished up to isomorphism only by their size. Thus the age of any DLO is countable. This shows in a way that a DLO is a kind of limit of finite linear orderings.
One can easily see that any class K which is an age of some structure satisfies the following two conditions:
Hereditary property: If A ∈ K and B is a finitely generated substructure of A, then B is isomorphic to a structure in K
Joint embedding property: If A and B are in K then there is C in K such that both A and B are embeddable in C.
Fraïssé proved that when K is any non-empty countable set of finitely generated σ-structures (with σ a signature
) which has the above two properties, then it is an age of a countable structure.
Furthermore, suppose that K happens to satisfy the following additional property.
Amalgamation property
: For any structures A, B and C in K such that A is embeddable in both B and C, there exists D in K to which B and C are both embeddable by embeddings which coincide on the image of A in both structures.
In that case there is a unique up to isomorphism structure which is countable, has the age K and is homogeneous. Homogeneous means here that any isomorphism between two finitely generated substructures can be extended to an automorphism. Again an example of this situation could be the ordered set of rational numbers
. It is the unique (up to isomorphism) homogenous countable structure whose age is the set of all finite linear orderings. Note that the ordered set of natural numbers 
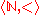has the same age as a DLO, but it is not homogenous since if we map {1, 3} to {5, 6}, it would not extend to any automorphism f since there should be an element between 
and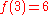 
. The same applies to integers.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, the age of a structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
(or model) A is the class of all finitely generated structures which are embeddable
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in A (i.e. isomorphic to substructures of A). This concept is central in the construction of a Fraïssé
Roland Fraïssé
Roland Fraïssé was a French mathematical logician. He received his doctoral degree from the University of Paris in 1953. In his thesis, Fraïssé used the back-and-forth method to determine whether two model-theoretic structures were elementarily equivalent...
limit.
The main point of Fraïssé's construction is to show how one can approximate a structure by its finitely generated substructures. Thus for example the age of any dense linear order without endpoints (DLO),
is precisely the set of all finite linear orderings, which are distinguished up to isomorphism only by their size. Thus the age of any DLO is countable. This shows in a way that a DLO is a kind of limit of finite linear orderings.One can easily see that any class K which is an age of some structure satisfies the following two conditions:
Hereditary property: If A ∈ K and B is a finitely generated substructure of A, then B is isomorphic to a structure in K
Joint embedding property: If A and B are in K then there is C in K such that both A and B are embeddable in C.
Fraïssé proved that when K is any non-empty countable set of finitely generated σ-structures (with σ a signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
) which has the above two properties, then it is an age of a countable structure.
Furthermore, suppose that K happens to satisfy the following additional property.
Amalgamation property
Amalgamation property
In the mathematical field of model theory, the amalgamation property is a property of collections of structures that guarantees, under certain conditions, that two structures in the collection can be regarded as substructures of a larger one....
: For any structures A, B and C in K such that A is embeddable in both B and C, there exists D in K to which B and C are both embeddable by embeddings which coincide on the image of A in both structures.
In that case there is a unique up to isomorphism structure which is countable, has the age K and is homogeneous. Homogeneous means here that any isomorphism between two finitely generated substructures can be extended to an automorphism. Again an example of this situation could be the ordered set of rational numbers
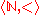. It is the unique (up to isomorphism) homogenous countable structure whose age is the set of all finite linear orderings. Note that the ordered set of natural numbers has the same age as a DLO, but it is not homogenous since if we map {1, 3} to {5, 6}, it would not extend to any automorphism f since there should be an element between and 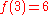. The same applies to integers.