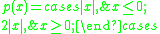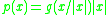Asymmetric norm
Encyclopedia
In mathematics
, an asymmetric norm on a vector space
is a generalization of the concept of a norm
.
vector space. Then an asymmetric norm on X is a function
p : X → R satisfying the following properties:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an asymmetric norm on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is a generalization of the concept of a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
.
Definition
Let X be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space. Then an asymmetric norm on X is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
p : X → R satisfying the following properties:
- non-negativity: for all x ∈ X, p(x) ≥ 0;
- definiteness: for x ∈ X, x = 0 if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
p(x) = p(−x) = 0; - homogeneityHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
: for all x ∈ X and all λ ≥ 0, p(λx) = λp(x); - the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
: for all x, y ∈ X, p(x + y) ≤ p(x) + p(y).
Examples
- On the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R, the function p given by
- is an asymmetric norm but not a norm.
- More generally, given a strictly positive function g : Sn−1 → R defined on the unit sphereUnit sphereIn mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
Sn−1 in Rn (with respect to the usual Euclidean norm |·|, say), the function p given by
- is an asymmetric norm on Rn but not necessarily a norm.