Bigraph
Encyclopedia
A bigraph can be modelled as the superposition of a graph
(the link graph) and a set of trees (the place graph).
Each node of the bigraph is part of a graph and also part of some tree that describes how the nodes are nested. Bigraphs can be conveniently and formally displayed as diagram
s. They have applications in the modelling of distributed systems for ubiquitous computing
and can be used to describe mobile
interactions. They have also been used by Robin Milner
in an attempt to subsume Calculus of Communicating Systems
(CCS) and π-calculus. They have been studied in the context of category theory
.
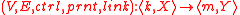
Where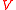
is a set of nodes, 
is a set of edges, 
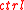is the control map that assigns controls to nodes, 
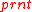is the parent map that defines the nesting of nodes, and 
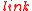is the link map that defines the link structure.
The notation
indicates that the bigraph has 
holes (sites) and a set of inner names 
and 
regions, with a set of outer names 
. These are respectively known as the inner and outer interfaces of the bigraph.
Formally speaking, each bigraph is an arrow in a symmetric partial monoidal category
(usually abbreviated spm-category) in which the objects are these interfaces. As a result, the composition of bigraphs is definable in terms of the composition of arrows in the category.
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
(the link graph) and a set of trees (the place graph).
Each node of the bigraph is part of a graph and also part of some tree that describes how the nodes are nested. Bigraphs can be conveniently and formally displayed as diagram
Diagram
A diagram is a two-dimensional geometric symbolic representation of information according to some visualization technique. Sometimes, the technique uses a three-dimensional visualization which is then projected onto the two-dimensional surface...
s. They have applications in the modelling of distributed systems for ubiquitous computing
Ubiquitous computing
Ubiquitous computing is a post-desktop model of human-computer interaction in which information processing has been thoroughly integrated into everyday objects and activities. In the course of ordinary activities, someone "using" ubiquitous computing engages many computational devices and systems...
and can be used to describe mobile
Mobile agent
In computer science, a mobile agent is a composition of computer software and data which is able to migrate from one computer to another autonomously and continue its execution on the destination computer.-Definition and overview:...
interactions. They have also been used by Robin Milner
Robin Milner
Arthur John Robin Gorell Milner FRS FRSE was a prominent British computer scientist.-Life, education and career:...
in an attempt to subsume Calculus of Communicating Systems
Calculus of Communicating Systems
The Calculus of Communicating Systems is a process calculus introduced by Robin Milner around 1980 and the title of a book describing the calculus. Its actions model indivisible communications between exactly two participants. The formal language includes primitives for describing parallel...
(CCS) and π-calculus. They have been studied in the context of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Anatomy of a bigraph
Aside from nodes and (hyper-)edges, a bigraph may have associated with it one or more regions which are roots in the place forest, and zero or more holes in the place graph, into which other bigraph regions may be inserted. Similarly, to nodes we may assign controls that define identities and an arity (the number of ports for a given node to which link-graph edges may connect). These controls are drawn from a bigraph signature. In the link graph we define inner and outer names, which define the connection points at which coincident names may be fused to form a single link.Foundations
A bigraph is a 5-tuple: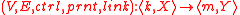Where
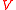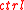is a set of nodes, is a set of edges, is the control map that assigns controls to nodes, 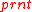is the parent map that defines the nesting of nodes, and 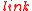is the link map that defines the link structure.The notation
indicates that the bigraph has holes (sites) and a set of inner names and regions, with a set of outer names . These are respectively known as the inner and outer interfaces of the bigraph.Formally speaking, each bigraph is an arrow in a symmetric partial monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
(usually abbreviated spm-category) in which the objects are these interfaces. As a result, the composition of bigraphs is definable in terms of the composition of arrows in the category.