
Biordered set
Encyclopedia
A biordered set is a mathematical object
that occurs in the description of the structure
of the set of idempotents in a semigroup
. The concept
and the terminology
were developed by K S S Nambooripad of Kerala
, India
, in the early 1970s.
The defining properties of a biordered set are expressed in terms of two quasiorders defined on the set and hence the name biordered set. Patrick Jordan, while a master's student at University of Sydney, introduced in 2002 the term boset as an abbreviation of biordered set.
"The axioms defining a biordered set are quite complicated. However, considering the general nature of semigroups, it is rather surprising that such a finite axiomatization is even possible." Since the publication of the original definition of the biordered set by Nambooripad, several variations in the definition have been proposed. David Easdown simplified the definition and formulated the axioms in a special arrow notation invented by him.
The set of idempotents in a semigroup is a biordered set and every biordered set is the set of idempotents of some semigroup.
A regular biordered set is a biordered set with an additional property. The set of idempotents in a regular semigroup
is a regular biordered set, and every regular biordered set is the set of idempotents of some regular semigroup.
Let E be a set in which a partial
binary operation
, indicated by juxtaposition, is defined. If DE is the domain
of the partial binary operation on E then DE is a relation
on E and (e,f) is in DE if and only if the product ef exists in E. The following relations can be defined in E:
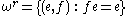
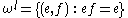
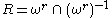
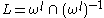
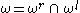
If T is any statement about E involving the partial binary operation and the above relations in E, one can define the left-right dual
of T denoted by T*. If DE is symmetric
then T* is meaningful whenever T is.
s and their duals hold for arbitrary elements e, f, g, etc in E.
ωr and ωl are reflexive
and transitive
relations on E and DE = ( ωr ∪ ω l ) ∪ ( ωr ∪ ωl )−1.
If f is in ωr( e ) then f R fe ω e.
If g ωl f and if f and g are in ωr ( e ) then ge ωl fe.
If g ωr f and f ωr e then gf = ( ge )f.
If g ωl f and if f and g are in ωr ( e ) then ( fg )e = ( fe )( ge ).
In M ( e, f ) = ωl ( e ) ∩ ωr ( f ), define a relation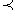 by
by
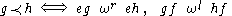 .
.
Then the set
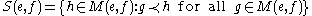
is called the sandwich set of e and f in that order.
If f and g are in ωr ( e ) then S( f, g )e = S ( fe, ge ).
For any e in E the sets ωr ( e ), ωl ( e ) and ω ( e ) are biordered subsets of E.
and
where V = A ⊕ B means that A and B are subspace
s of V and V is the internal direct sum of A and B.
The partial binary operation ⋆ on E defined by
⋆ ( C, D ) = ( A + ( B ∩ C ), ( B + C ) ∩ D )
makes E a biordered set. The quasiorders in E are characterised as follows:
ωr ( C, D ) ⇔ A ⊇ C ωl ( C, D ) ⇔ B ⊆ D
As a concrete example, let S be the semigroup of all mappings of X = { 1, 2, 3 } into itself. Let the symbol (abc) denote the map for which 1 → a , 2 → b , and 3 → c. The set E of idempotents in S contains the following elements:
, (222), (333) (constant maps)
, (133), (121), (323), (113), (223)
(identity map)
The following table (taking composition of mappings in the diagram order) describes the partial binary operation in E. An X in a cell indicates that the corresponding multiplication is not defined.
Mathematical object
In mathematics and the philosophy of mathematics, a mathematical object is an abstract object arising in mathematics.Commonly encountered mathematical objects include numbers, permutations, partitions, matrices, sets, functions, and relations...
that occurs in the description of the structure
Structure
Structure is a fundamental, tangible or intangible notion referring to the recognition, observation, nature, and permanence of patterns and relationships of entities. This notion may itself be an object, such as a built structure, or an attribute, such as the structure of society...
of the set of idempotents in a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
. The concept
Concept
The word concept is used in ordinary language as well as in almost all academic disciplines. Particularly in philosophy, psychology and cognitive sciences the term is much used and much discussed. WordNet defines concept: "conception, construct ". However, the meaning of the term concept is much...
and the terminology
Terminology
Terminology is the study of terms and their use. Terms are words and compound words that in specific contexts are given specific meanings, meanings that may deviate from the meaning the same words have in other contexts and in everyday language. The discipline Terminology studies among other...
were developed by K S S Nambooripad of Kerala
Kerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
, India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
, in the early 1970s.
The defining properties of a biordered set are expressed in terms of two quasiorders defined on the set and hence the name biordered set. Patrick Jordan, while a master's student at University of Sydney, introduced in 2002 the term boset as an abbreviation of biordered set.
"The axioms defining a biordered set are quite complicated. However, considering the general nature of semigroups, it is rather surprising that such a finite axiomatization is even possible." Since the publication of the original definition of the biordered set by Nambooripad, several variations in the definition have been proposed. David Easdown simplified the definition and formulated the axioms in a special arrow notation invented by him.
The set of idempotents in a semigroup is a biordered set and every biordered set is the set of idempotents of some semigroup.
A regular biordered set is a biordered set with an additional property. The set of idempotents in a regular semigroup
Regular semigroup
A regular semigroup is a semigroup S in which every element is regular, i.e., for each element a, there exists an element x such that axa = a. Regular semigroups are one of the most-studied classes of semigroups, and their structure is particularly amenable to study via Green's relations.- Origins...
is a regular biordered set, and every regular biordered set is the set of idempotents of some regular semigroup.
Definition
The formal definition of a biordered set given by Nambooripad requires some preliminaries.Preliminaries
If X and Y be sets and ρ⊆ X × Y, let ρ ( y ) = { x ∈ X : x ρ y }.Let E be a set in which a partial
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, indicated by juxtaposition, is defined. If DE is the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of the partial binary operation on E then DE is a relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
on E and (e,f) is in DE if and only if the product ef exists in E. The following relations can be defined in E:
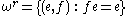
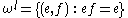
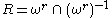
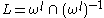
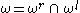
If T is any statement about E involving the partial binary operation and the above relations in E, one can define the left-right dual
Dual
Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...
of T denoted by T*. If DE is symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
then T* is meaningful whenever T is.
Formal definition
The set E is called a biordered set if the following axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s and their duals hold for arbitrary elements e, f, g, etc in E.
ωr and ωl are reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
relations on E and DE = ( ωr ∪ ω l ) ∪ ( ωr ∪ ωl )−1.
If f is in ωr( e ) then f R fe ω e.
If g ωl f and if f and g are in ωr ( e ) then ge ωl fe.
If g ωr f and f ωr e then gf = ( ge )f.
If g ωl f and if f and g are in ωr ( e ) then ( fg )e = ( fe )( ge ).
In M ( e, f ) = ωl ( e ) ∩ ωr ( f ), define a relation
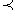 by
by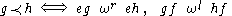 .
.Then the set
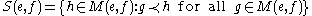
is called the sandwich set of e and f in that order.
If f and g are in ωr ( e ) then S( f, g )e = S ( fe, ge ).
Regular biordered set
A biordered set E is called a regular biordered set if S ( e, f ) ≠ ∅ for all e and f in E.Biordered subsets
A subset F of a biordered set E is a biordered subset (subboset) of E if F is a biordered set under the partial binary operation inherited from E.For any e in E the sets ωr ( e ), ωl ( e ) and ω ( e ) are biordered subsets of E.
Bimorhisms
A mapping φ : E → F between two biordered sets E and F is a biordered set homomorphism (also called a bimorphism) if for all ( e, f ) in DE we have ( eφ ) ( fφ ) = ( ef )φ.Vector space example
Let V be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and
- E = { ( A, B ) | V = A ⊕ B }
where V = A ⊕ B means that A and B are subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
s of V and V is the internal direct sum of A and B.
The partial binary operation ⋆ on E defined by
⋆ ( C, D ) = ( A + ( B ∩ C ), ( B + C ) ∩ D )
makes E a biordered set. The quasiorders in E are characterised as follows:
ωr ( C, D ) ⇔ A ⊇ C ωl ( C, D ) ⇔ B ⊆ D
Biordered set of a semigroup
The set E of idempotents in a semigroup S becomes a biordered set if a partial binary operation is defined in E as follows: ef is defined in E if and only if ef = e or ef= f or fe = e or fe = f holds in S. If S is a regular semigroup then E is a regular biordered set.As a concrete example, let S be the semigroup of all mappings of X = { 1, 2, 3 } into itself. Let the symbol (abc) denote the map for which 1 → a , 2 → b , and 3 → c. The set E of idempotents in S contains the following elements:
, (222), (333) (constant maps)
, (133), (121), (323), (113), (223)
(identity map)
The following table (taking composition of mappings in the diagram order) describes the partial binary operation in E. An X in a cell indicates that the corresponding multiplication is not defined.
| ∗ | (111) | (222) | (333) | (122) | (133) | (121) | (323) | (113) | (223) | (123) |
|---|---|---|---|---|---|---|---|---|---|---|
| (111) | (111) | (222) | (333) | (111) | (111) | (111) | (333) | (111) | (222) | (111) |
| (222) | (111) | (222) | (333) | (222) | (333) | (222) | (222) | (111) | (222) | (222) |
| (333) | (111) | (222) | (333) | (222) | (333) | (111) | (333) | (333) | (333) | (333) |
| (122) | (111) | (222) | (333) | (122) | (122) | (121) | X | X | X | (122) |
| (133) | (111) | (222) | (333) | (122) | (133) | X | X | (133) | X | (133) |
| (121) | (111) | (222) | (333) | (121) | X | (121) | (323) | X | X | (121) |
| (323) | (111) | (222) | (333) | X | X | (121) | (323) | X | (323) | (323) |
| (113) | (111) | (222) | (333) | X | (113) | X | X | (113) | (223) | (113) |
| (223) | (111) | (222) | (333) | X | X | X | (233) | (113) | (223) | (223) |
| (123) | (111) | (222) | (333) | (122) | (133) | (121) | (323) | (113) | (223) | (123) |

