Chien's search
Encyclopedia
In abstract algebra
, the Chien search, named after R. T. Chien, is a fast algorithm for determining roots of polynomial
s defined over a finite field
. The most typical use of the Chien search is in finding the roots of error-locator polynomials encountered in decoding Reed-Solomon codes and BCH code
s.
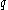)) whose roots we wish to determine as:
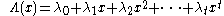
Conceptually, we may evaluate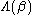
for each non-zero 
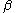in GF(
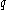). Those resulting in 0 are roots of the polynomial.
The Chien search is based on two observations:
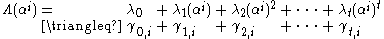
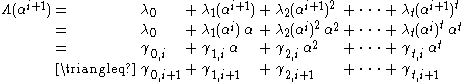
In other words, we may define each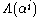
as the sum of a set of terms 
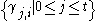, from which the next set of coefficients may be derived thus:
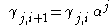
In this way, we may start at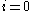
with 
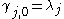, and iterate through each value of 
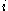up to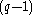 
. If at any stage the resultant summation is zero, i.e.
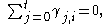
then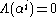
also, so 
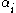is a root. In this way, we check every element in the field.
When implemented in hardware, this approach significantly reduces the complexity, as all multiplications consist of one variable and one constant, rather than two variables as in the brute-force approach.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the Chien search, named after R. T. Chien, is a fast algorithm for determining roots of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s defined over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. The most typical use of the Chien search is in finding the roots of error-locator polynomials encountered in decoding Reed-Solomon codes and BCH code
BCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s.
Algorithm
We denote the polynomial (over the finite field GF(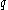)) whose roots we wish to determine as: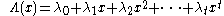Conceptually, we may evaluate
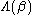for each non-zero 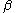in GF(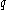). Those resulting in 0 are roots of the polynomial.The Chien search is based on two observations:
- Each non-zero
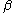may be expressed as 
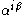for some 
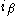, where 
is a primitive element of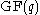 
. Thus the powers 
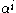for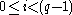 
cover the entire field (excluding the zero element).
- The following relationship exists:
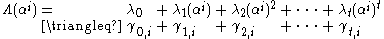
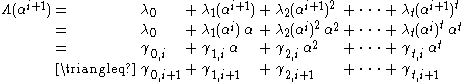
In other words, we may define each
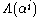as the sum of a set of terms 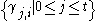, from which the next set of coefficients may be derived thus: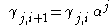In this way, we may start at
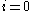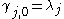with , and iterate through each value of 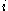up to 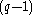. If at any stage the resultant summation is zero, i.e.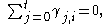then
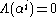also, so 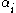is a root. In this way, we check every element in the field.When implemented in hardware, this approach significantly reduces the complexity, as all multiplications consist of one variable and one constant, rather than two variables as in the brute-force approach.