
Cunningham correction factor
Encyclopedia
The Cunningham correction factor or Cunningham slip correction factor is used to account for noncontinuum effects when calculating the drag on small particles. The derivation of Stokes Law
, which is used to calculate the drag force on small particles, assumes a No-slip condition
which is no longer correct at high Knudsen number
. The Cunningham slip correction factor allows predicting the drag force on a particle moving a fluid with Knudsen number
between the continuum regime and free molecular flow
.
drag coefficient
calculated with standard correlations is divided by the Cunningham correction factor, C given below.
Ebenezer Cunningham
derived the correction factor in 1910 and verified with Robert Andrews Millikan the correction in the same year.
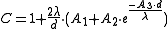
where
The Cunningham correction factor becomes significant when particles become smaller than 15 micrometers, for air at ambient conditions.
For sub-micrometer particles, Brownian motion
must be taken into account.
Stokes law
Stokes' law can refer to:*Stokes' law for friction force*Stokes' law law describing attenuation of sound in Newtonian liquidsFor integration, see Stokes' theorem....
, which is used to calculate the drag force on small particles, assumes a No-slip condition
No-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
which is no longer correct at high Knudsen number
Knudsen number
The Knudsen number is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid...
. The Cunningham slip correction factor allows predicting the drag force on a particle moving a fluid with Knudsen number
Knudsen number
The Knudsen number is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid...
between the continuum regime and free molecular flow
Free molecular flow
Free molecular flow describes the fluid dynamics of gas where the mean free path of the molecules is larger than the size of the chamber or of the object under test. For tubes/objects of the size of several cm, these means pressures well below 10-3 torr. This is also called the regime of high...
.
drag coefficient
Drag coefficient
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
calculated with standard correlations is divided by the Cunningham correction factor, C given below.
Ebenezer Cunningham
Ebenezer Cunningham
Ebenezer Cunningham was a British mathematician who is remembered for his research and exposition at the dawn of special relativity....
derived the correction factor in 1910 and verified with Robert Andrews Millikan the correction in the same year.
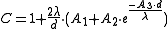
where
- C is the correction factor
- λ is the mean free pathMean free pathIn physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
- d is the particle diameter
- An are experimentally determined coefficients.
- For air (Davies, 1945):
- A1 = 1.257
- A2 = 0.400
- A3 = 0.55
The Cunningham correction factor becomes significant when particles become smaller than 15 micrometers, for air at ambient conditions.
For sub-micrometer particles, Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
must be taken into account.

