Cybernetical physics
Encyclopedia
Cybernetical physics is a scientific area on the border of Cybernetics
and Physics
which studies physical systems with cybernetics methods. Cybernetics
methods are understood as methods developed within control theory
, information theory
, systems theory
and related areas: control design, estimation
, identification
, optimization
, pattern recognition
, signal processing
, image processing
, etc. Physical systems are also understood in a broad sense: either lifeless or living nature
or of artificial (engineering) origin, having reasonably understood dynamics and models suited for posing cybernetical problems. Research objectives in cybernetical physics are frequently formulated as analyses of a class of possible system state changes under external (controlling) actions of a certain class. An auxiliary goal is design of controlling actions required to achieve prespecified property change. Among typical control action classes are functions which are constant in time (bifurcation analysis, optimization), functions which depend only on time (vibration
mechanics, spectroscopic studies
, program control), and functions whose value depends on measurement results at the same time or previous instants. The last class is of special interest since these functions correspond to system analysis by means of external feedback
(feedback control).
and quantum control.
exceeded 4000 by the beginning of the 21st century. The number of papers published in peer reviewed journals achieved 300-400 papers per year. The method proposed in is now called the OGY-method after the authors' initials.
Later a number of other methods were proposed for transformation of chaotic trajectories into periodic ones? E.g. delayed feedback (Pyragas method) . Numerous nonlinear and adaptive control methods were also applied for control of chaos, see surveys in .
It is important that the results obtained were interpreted as discovering new properties of physical systems. Thousands of papers were published that examine and predict properties of systems based on using control, identification and other cybernetic methods. Notably, an overwhelming part of those papers were published in physical journals, their authors were representing physical departments of the universities. It has become clear that such type of control goals are important not only for control of chaos, but also for control of a broader class of oscillatory processes. This provides evidence for the existence of the new emerging field of research related to both physics and control, that of ‘’’Cybernetical Physics’’’ ,
were seeking ways to change a natural course of chemical reactions whilst attempting to transform lead into gold. The next milestone was set by the famous British physicist James Clerk Maxwell
. In 1871 he introduced a hypothetical being, known under the name Maxwell's Demon
with ability to measure velocities of gas molecules and to direct fast molecules to one part of the vessel, keeping slow molecules in the other part. It produces a temperature difference between the two parts of the vessel which seems to contradict the Second Law of thermodynamics
. Now, after more than a century of fruitful life, Demon is even more active than in the past. In recent papers the issues of experimental implementation of the Maxwell's Demon
are discussed, particularly at the quantum-mechanical level .
In the end of the 1970s the first mathematical results for control of quantum mechanical models were established based on control theory
In the end of the 1980s—beginning of the 1990s rapid development of laser industry led to appearance of ultrafast, the so called femtosecond lasers. A new generation of lasers
have the ability to generate pulses with duration of about a few femtoseconds and even less (1 fs =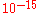
sec). The duration of such a pulse is comparable with the period of a molecule's natural oscillation. Therefore, femtosecond laser can be, in principle, used as a mean for control of single molecules and atoms. A consequence of such an application is a possibility of realizing an alchemists' dream to change the natural course of chemical reactions. A new area in chemistry emerged – femtochemistry
and new femtotechnologies
were developed. Ahmed Zewail
from Caltech was awarded with the 1999 Nobel Prize in Chemistry for his work on femtochemistry
.
Using the apparatus of modern control theory, new horizons in studying interaction of atoms and molecules may open and new ways and possible limits for intervention into intimate processes of the microworld may be discovered. Besides, control is an important part of many recent nanoscale applications: nanomotors, nanowires, nanochips, nanorobots, etc. The number of publications in the peer reviewed journals per year exceeds 600.
in 1824. He considered a heat engine which operates by drawing heat from a source which is at thermal equilibrium at temperature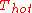
, and delivering useful work. Carnot saw that, in order to operate continuously, the engine requires also a cold reservoir with the temperature 
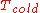, to which some heat can be discharged. By simple logic he established the famous
‘’’Carnot's Principle’’’: ‘’No heat engine can be more efficient than a reversible one operating between the same temperatures’’.
In fact it was nothing but the solution to an optimal control
problem: maximum work can be extracted by a reversible machine and the value of extracted work depends only on the temperatures of the source and the bath. Later Kelvin introduced his absolute temperature scale (Kelvin scale) and accomplished the next step, evaluating the Carnot's reversible efficiency
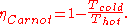
However, most works were devoted to study of stationary systems over infinite time interval, while for practical purposes it is important to know possibilities and limitations of
the system evolution for finite times as well as under other types of constraints caused by a finite amount of resources available.
The pioneer works devoted to evaluation of finite time limitations for heat engines were published by I.Novikov in 1957 and, independently by F.L.Curzon and B.Ahlborn in 1975 that the efficiency at maximum power per cycle of a heat engine coupled to its surroundings through a constant heat conductor is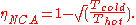
(Novikov-Curzon-Ahlborn formula).
Note the Novikov-Curzon-Ahlborn process is also optimal in the sense of minimal dissipation. Otherwise, if the dissipation degree is given, the process corresponds to the maximum entropy principle. Later the results were extended and generalized for other criteria and for more complex situations based on the modern optimal control theory
. As a result a new direction in thermodynamics arose known under the names ‘’optimization thermodynamics’’, ‘’finite-time thermodynamics’’, Endoreversible thermodynamics
or
'’control thermodynamics’’ see .
Description of the control problems related to cybernetical physics includes classes of controlled plant models, control objectives (goals) and admissible control algorithms. The methodology of cybernetical physics, comprises typical methods used for solving the problems and typical results in the field.
controlled (plant) and a model of the control objective (goal). Even if the plant model is not given (like in many real world applications) it should be determined in some way. The system models used in cybernetics are similar to traditional models of physics and mechanics with one difference; the inputs and outputs of the model should be explicitly specified. The following main classes of models are considered in the literature related to control of physical systems: continuous systems with lumped parameters described in state space by differential equations; distributed (spatio-temporal) systems described by partial differential equations; discrete-time state-space models described by difference equations.
Regulation (often called stabilization or positioning) is the most common and simple control goal. Regulation is understood as driving the state vector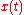
(or the output vector
) to some equilibrium state
(respectively, 
).
Tracking. State tracking is driving a solution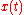
to the prespecified function of time
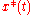. Similarly, output tracking is driving the output
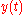to the desired output function
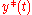. The problem is more complex if the desired equilibrium 
or trajectory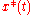 
are unstable in the absence of control action. For example, a typical problem of chaos control can be formulated as tracking of an unstable periodic solution (orbit). The key feature of the control problems for physical systems is that the goal should be achieved by means of sufficiently small control. A limit case is stabilization of a system by an arbitrarily small control. Solvability of this task is not obvious if the trajectory 
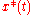is unstable, like for the case of chaotic systems, see .
Generation (excitation) of oscillations. The third class of control goals corresponds to the problems of ‘’excitation’’ or ‘’generation’’ of oscillations. Here, it is assumed that the system is initially at rest. The problem is to find out if it is possible to drive it into an
oscillatory mode with the desired characteristics (energy, frequency, etc.) In this case the goal trajectory of the state vector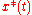
is not prespecified. Moreover, the goal trajectory may be unknown, or may even be irrelevant to the achievement of the control goal. Such problems are well known in electrical, radio engineering, acoustics, laser and vibrational technologies—wherever it is necessary to create an oscillatory mode for the system. Such a class of control goals can be related to problems of dissociation, ionization of molecular systems, escape from a potential well, chaotization and other problems related to growth of the system energy and its possible phase transition. Sometimes such problems can be reduced to tracking, but the reference trajectories 
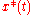in these cases are not necessarily periodic and may be unstable. Besides, the goal trajectory 
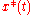may be known only partially.
Synchronization. The fourth important class of control goals corresponds to synchronization (more accurately, ‘’controlled synchronization’’ as distinct from
‘’autosynchronization’’ or ‘’self-synchronization’’). Generally speaking, synchronization is understood as concurrent change of the states of two or more systems or, perhaps, concurrent change of some quantities related to the systems, e.g. equalizing of oscillation frequencies. If the required relation is established only asymptotically, one speaks about ‘’asymptotic synchronization’’. If synchronization does not exist in the system without control we may pose the problem as finding the control function which ensures synchronization in the closed-loop system, i.e. synchronization may be a control goal. Synchronization problem differs from the model reference control problem in that some phase shifts between the processes are allowed that are either constant or tend to constant values. Besides, in a number of synchronization problems the links between the systems to be synchronized are bidirectional ones. In such cases the limit mode (synchronous mode) in the overall system is not known in advance.
Modification of the limit sets (attractor
s) of the systems. The last class of the control goals is related to modification of some quantitative characteristics of the limit behavior of the system. It includes such specific goals as
Investigation of the above problems started in the end of the 1980s with the works on bifurcation
control and continued in the works on control of chaos. Ott, Grebogi and Yorke and their followers introduced a new class of control goals, not requiring any quantitative characteristic of the desired motion. Instead, the desired qualitative type of the limit set (attractor
) was specified, e.g. control should provide the system with a chaotic attractor. Additionally, the desired degree of chaoticity may be specified by means of specifying Lyapunov exponent
, fractal dimension
, entropy
, etc. see .
In addition to the main control goal some additional goals or constraints may be specified. A typical example is the ``small control" requirements: control function should have small power or should provide small expenditure of energy. Such a restriction is needed to avoid ``violence" and preserve inherent properties of the system under control. This is important to ensure elimination of artefacts and adequate study of the system.
Three types of control are used in physical problems: constant control, feedforward control and feedback control. Implementation of a feedback control requires additional measurement devices working in real time which are often hard to install. Therefore, studying the system may start with application of inferior forms of control: time-constant and then feedforward control. The possibilities of changing the system behavior by means of feedback control can then be studied.
. Typically, some parameters of physical systems are unknown and some variables are not available for measurement. From the control viewpoint this means that control design should be
performed under significant uncertainty, i.e. methods of robust control
or adaptive control
should be used. A variety of design methods
have been developed by control theorists and control engineers
for both linear and nonlinear systems. Methods of partial control, control by weak signals, etc. have also been developed.
The following areas of research are being developed actively :
Among most important applications are: control of fusion
, control of beams, control in nano- and femtotechnologies.
In order to facilitate information exchange in the area of cybernetical physics the International Physics and Control Society (IPACS) was created
The IPACS organizes regular conferences (Physics and Control Conferences), supports electronic library IPACS Electronic Library and information portal Physics and Control Resources.
Cybernetics
Cybernetics is the interdisciplinary study of the structure of regulatory systems. Cybernetics is closely related to information theory, control theory and systems theory, at least in its first-order form...
and Physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
which studies physical systems with cybernetics methods. Cybernetics
Cybernetics
Cybernetics is the interdisciplinary study of the structure of regulatory systems. Cybernetics is closely related to information theory, control theory and systems theory, at least in its first-order form...
methods are understood as methods developed within control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, systems theory
Systems theory
Systems theory is the transdisciplinary study of systems in general, with the goal of elucidating principles that can be applied to all types of systems at all nesting levels in all fields of research...
and related areas: control design, estimation
Estimation
Estimation is the calculated approximation of a result which is usable even if input data may be incomplete or uncertain.In statistics,*estimation theory and estimator, for topics involving inferences about probability distributions...
, identification
System identification
In control engineering, the field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data...
, optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
, signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, etc. Physical systems are also understood in a broad sense: either lifeless or living nature
Nature
Nature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
or of artificial (engineering) origin, having reasonably understood dynamics and models suited for posing cybernetical problems. Research objectives in cybernetical physics are frequently formulated as analyses of a class of possible system state changes under external (controlling) actions of a certain class. An auxiliary goal is design of controlling actions required to achieve prespecified property change. Among typical control action classes are functions which are constant in time (bifurcation analysis, optimization), functions which depend only on time (vibration
Vibration
Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodic such as the motion of a pendulum or random such as the movement of a tire on a gravel road.Vibration is occasionally "desirable"...
mechanics, spectroscopic studies
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
, program control), and functions whose value depends on measurement results at the same time or previous instants. The last class is of special interest since these functions correspond to system analysis by means of external feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
(feedback control).
Roots of cybernetical physics
Until recently no creative interaction of physics and control theory (cybernetics) has been seen and no control theory methods have been directly used for discovering new physical effects and phenomena. The situation has dramatically changed in the 1990s when two new areas emerged: control of chaosControl of chaos
In chaos theory, control of chaos is based on the fact that any chaotic attractor contains an infinite number of unstable periodic orbits. Chaotic dynamics then consists of a motion where the system state moves in the neighborhood of one of these orbits for a while, then falls close to a different...
and quantum control.
Control of chaos
In 1990 the paper was published in Physical Review Letters by Edward Ott, Celso Grebogi and James Yorke from the University of Maryland discovered that even small feedback action can dramatically change behavior of a nonlinear system, e.g. turn chaotic motions into periodic ones and vice versa. The idea became popular in the physics community almost immediately and since 1990 hundreds of papers were published demonstrating the ability of small control, with or without feedback, to change dynamics of real or model systems significantly. By 2003, the Ott, Grebogi and Yorke's paper has been quoted over 1300 times whilst the total number of the papers relating to control of chaosControl of chaos
In chaos theory, control of chaos is based on the fact that any chaotic attractor contains an infinite number of unstable periodic orbits. Chaotic dynamics then consists of a motion where the system state moves in the neighborhood of one of these orbits for a while, then falls close to a different...
exceeded 4000 by the beginning of the 21st century. The number of papers published in peer reviewed journals achieved 300-400 papers per year. The method proposed in is now called the OGY-method after the authors' initials.
Later a number of other methods were proposed for transformation of chaotic trajectories into periodic ones? E.g. delayed feedback (Pyragas method) . Numerous nonlinear and adaptive control methods were also applied for control of chaos, see surveys in .
It is important that the results obtained were interpreted as discovering new properties of physical systems. Thousands of papers were published that examine and predict properties of systems based on using control, identification and other cybernetic methods. Notably, an overwhelming part of those papers were published in physical journals, their authors were representing physical departments of the universities. It has become clear that such type of control goals are important not only for control of chaos, but also for control of a broader class of oscillatory processes. This provides evidence for the existence of the new emerging field of research related to both physics and control, that of ‘’’Cybernetical Physics’’’ ,
Quantum Control
It is conceivable that molecular physics was the area where ideas of control appeared first. One may trace its roots back to the Middle Ages, where alchemistsAlchemy
Alchemy is an influential philosophical tradition whose early practitioners’ claims to profound powers were known from antiquity. The defining objectives of alchemy are varied; these include the creation of the fabled philosopher's stone possessing powers including the capability of turning base...
were seeking ways to change a natural course of chemical reactions whilst attempting to transform lead into gold. The next milestone was set by the famous British physicist James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
. In 1871 he introduced a hypothetical being, known under the name Maxwell's Demon
Maxwell's demon
In the philosophy of thermal and statistical physics, Maxwell's demon is a thought experiment created by the Scottish physicist James Clerk Maxwell to "show that the Second Law of Thermodynamics has only a statistical certainty." It demonstrates Maxwell's point by hypothetically describing how to...
with ability to measure velocities of gas molecules and to direct fast molecules to one part of the vessel, keeping slow molecules in the other part. It produces a temperature difference between the two parts of the vessel which seems to contradict the Second Law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
. Now, after more than a century of fruitful life, Demon is even more active than in the past. In recent papers the issues of experimental implementation of the Maxwell's Demon
Maxwell's demon
In the philosophy of thermal and statistical physics, Maxwell's demon is a thought experiment created by the Scottish physicist James Clerk Maxwell to "show that the Second Law of Thermodynamics has only a statistical certainty." It demonstrates Maxwell's point by hypothetically describing how to...
are discussed, particularly at the quantum-mechanical level .
In the end of the 1970s the first mathematical results for control of quantum mechanical models were established based on control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
In the end of the 1980s—beginning of the 1990s rapid development of laser industry led to appearance of ultrafast, the so called femtosecond lasers. A new generation of lasers
have the ability to generate pulses with duration of about a few femtoseconds and even less (1 fs =
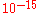sec). The duration of such a pulse is comparable with the period of a molecule's natural oscillation. Therefore, femtosecond laser can be, in principle, used as a mean for control of single molecules and atoms. A consequence of such an application is a possibility of realizing an alchemists' dream to change the natural course of chemical reactions. A new area in chemistry emerged – femtochemistryFemtochemistry
Femtochemistry is the science that studies chemical reactions on extremely short timescales, approximately 10–15 seconds .-Introduction:...
and new femtotechnologies
Femtotechnology
Femtotechnology is a hypothetical term used in reference to structuring of matter on a femtometer, which is 10-15 m. This is a smaller scale in comparison to nanotechnology and picotechnology which are 10-9 m and 10-12 m respectively...
were developed. Ahmed Zewail
Ahmed Zewail
Ahmed Hassan Zewail is an Egyptian-American scientist who won the 1999 Nobel Prize in Chemistry for his work on femtochemistry. He is the Linus Pauling Chair Professor Chemistry and Professor of Physics at the California Institute of Technology.- Birth and education :Ahmed Zewail was born on...
from Caltech was awarded with the 1999 Nobel Prize in Chemistry for his work on femtochemistry
Femtochemistry
Femtochemistry is the science that studies chemical reactions on extremely short timescales, approximately 10–15 seconds .-Introduction:...
.
Using the apparatus of modern control theory, new horizons in studying interaction of atoms and molecules may open and new ways and possible limits for intervention into intimate processes of the microworld may be discovered. Besides, control is an important part of many recent nanoscale applications: nanomotors, nanowires, nanochips, nanorobots, etc. The number of publications in the peer reviewed journals per year exceeds 600.
Control Thermodynamics
The basics of thermodynamics were stated by Sadi CarnotNicolas Léonard Sadi Carnot
Nicolas Léonard Sadi Carnot was a French military engineer who, in his 1824 Reflections on the Motive Power of Fire, gave the first successful theoretical account of heat engines, now known as the Carnot cycle, thereby laying the foundations of the second law of thermodynamics...
in 1824. He considered a heat engine which operates by drawing heat from a source which is at thermal equilibrium at temperature
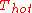, and delivering useful work. Carnot saw that, in order to operate continuously, the engine requires also a cold reservoir with the temperature 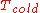, to which some heat can be discharged. By simple logic he established the famous‘’’Carnot's Principle’’’: ‘’No heat engine can be more efficient than a reversible one operating between the same temperatures’’.
In fact it was nothing but the solution to an optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
problem: maximum work can be extracted by a reversible machine and the value of extracted work depends only on the temperatures of the source and the bath. Later Kelvin introduced his absolute temperature scale (Kelvin scale) and accomplished the next step, evaluating the Carnot's reversible efficiency
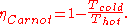
However, most works were devoted to study of stationary systems over infinite time interval, while for practical purposes it is important to know possibilities and limitations of
the system evolution for finite times as well as under other types of constraints caused by a finite amount of resources available.
The pioneer works devoted to evaluation of finite time limitations for heat engines were published by I.Novikov in 1957 and, independently by F.L.Curzon and B.Ahlborn in 1975 that the efficiency at maximum power per cycle of a heat engine coupled to its surroundings through a constant heat conductor is
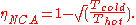
(Novikov-Curzon-Ahlborn formula).
Note the Novikov-Curzon-Ahlborn process is also optimal in the sense of minimal dissipation. Otherwise, if the dissipation degree is given, the process corresponds to the maximum entropy principle. Later the results were extended and generalized for other criteria and for more complex situations based on the modern optimal control theory
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
. As a result a new direction in thermodynamics arose known under the names ‘’optimization thermodynamics’’, ‘’finite-time thermodynamics’’, Endoreversible thermodynamics
Endoreversible thermodynamics
Endoreversible thermodynamics is a subset of irreversible thermodynamics aimed at making more realistic assumptions about heat transfer than are typically made in reversible thermodynamics...
or
'’control thermodynamics’’ see .
Subject and Methodology of Cybernetical Physics
By the end of the 1990s it has become clear that a new area in physics dealing with control methods has emerged. The term ‘’’cybernetical physics’’’ was proposed in. Subject and methodology of the field are systematically presented in .Description of the control problems related to cybernetical physics includes classes of controlled plant models, control objectives (goals) and admissible control algorithms. The methodology of cybernetical physics, comprises typical methods used for solving the problems and typical results in the field.
Models of Controlled Systems
A formal statement of any control problem begins with a model of the system to becontrolled (plant) and a model of the control objective (goal). Even if the plant model is not given (like in many real world applications) it should be determined in some way. The system models used in cybernetics are similar to traditional models of physics and mechanics with one difference; the inputs and outputs of the model should be explicitly specified. The following main classes of models are considered in the literature related to control of physical systems: continuous systems with lumped parameters described in state space by differential equations; distributed (spatio-temporal) systems described by partial differential equations; discrete-time state-space models described by difference equations.
Control Goals
It is natural to classify control problems by their control goals. We list here five kind of goals.Regulation (often called stabilization or positioning) is the most common and simple control goal. Regulation is understood as driving the state vector
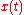(or the output vector) to some equilibrium state (respectively, ).Tracking. State tracking is driving a solution
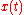to the prespecified function of time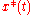. Similarly, output tracking is driving the output 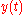to the desired output function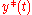. The problem is more complex if the desired equilibrium or trajectory 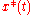are unstable in the absence of control action. For example, a typical problem of chaos control can be formulated as tracking of an unstable periodic solution (orbit). The key feature of the control problems for physical systems is that the goal should be achieved by means of sufficiently small control. A limit case is stabilization of a system by an arbitrarily small control. Solvability of this task is not obvious if the trajectory 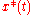is unstable, like for the case of chaotic systems, see .Generation (excitation) of oscillations. The third class of control goals corresponds to the problems of ‘’excitation’’ or ‘’generation’’ of oscillations. Here, it is assumed that the system is initially at rest. The problem is to find out if it is possible to drive it into an
oscillatory mode with the desired characteristics (energy, frequency, etc.) In this case the goal trajectory of the state vector
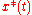is not prespecified. Moreover, the goal trajectory may be unknown, or may even be irrelevant to the achievement of the control goal. Such problems are well known in electrical, radio engineering, acoustics, laser and vibrational technologies—wherever it is necessary to create an oscillatory mode for the system. Such a class of control goals can be related to problems of dissociation, ionization of molecular systems, escape from a potential well, chaotization and other problems related to growth of the system energy and its possible phase transition. Sometimes such problems can be reduced to tracking, but the reference trajectories 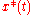in these cases are not necessarily periodic and may be unstable. Besides, the goal trajectory 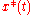may be known only partially.Synchronization. The fourth important class of control goals corresponds to synchronization (more accurately, ‘’controlled synchronization’’ as distinct from
‘’autosynchronization’’ or ‘’self-synchronization’’). Generally speaking, synchronization is understood as concurrent change of the states of two or more systems or, perhaps, concurrent change of some quantities related to the systems, e.g. equalizing of oscillation frequencies. If the required relation is established only asymptotically, one speaks about ‘’asymptotic synchronization’’. If synchronization does not exist in the system without control we may pose the problem as finding the control function which ensures synchronization in the closed-loop system, i.e. synchronization may be a control goal. Synchronization problem differs from the model reference control problem in that some phase shifts between the processes are allowed that are either constant or tend to constant values. Besides, in a number of synchronization problems the links between the systems to be synchronized are bidirectional ones. In such cases the limit mode (synchronous mode) in the overall system is not known in advance.
Modification of the limit sets (attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
s) of the systems. The last class of the control goals is related to modification of some quantitative characteristics of the limit behavior of the system. It includes such specific goals as
- changing the type of the equilibrium (e.g. transformation of an unstable equilibrium into a stable one or vice versa);
- changing the type of the limit set (e.g. transformation of a limit cycle into a chaotic attractor or vice versa, changing fractal dimension of the limit set, etc.);
- changing the position or the type of the bifurcationBifurcation theoryBifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
point in the parameter space of the system.
Investigation of the above problems started in the end of the 1980s with the works on bifurcation
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
control and continued in the works on control of chaos. Ott, Grebogi and Yorke and their followers introduced a new class of control goals, not requiring any quantitative characteristic of the desired motion. Instead, the desired qualitative type of the limit set (attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
) was specified, e.g. control should provide the system with a chaotic attractor. Additionally, the desired degree of chaoticity may be specified by means of specifying Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
, fractal dimension
Fractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
, entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
, etc. see .
In addition to the main control goal some additional goals or constraints may be specified. A typical example is the ``small control" requirements: control function should have small power or should provide small expenditure of energy. Such a restriction is needed to avoid ``violence" and preserve inherent properties of the system under control. This is important to ensure elimination of artefacts and adequate study of the system.
Three types of control are used in physical problems: constant control, feedforward control and feedback control. Implementation of a feedback control requires additional measurement devices working in real time which are often hard to install. Therefore, studying the system may start with application of inferior forms of control: time-constant and then feedforward control. The possibilities of changing the system behavior by means of feedback control can then be studied.
Methodology
The methodology of cybernetical physics is based on control theoryControl theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
. Typically, some parameters of physical systems are unknown and some variables are not available for measurement. From the control viewpoint this means that control design should be
performed under significant uncertainty, i.e. methods of robust control
Robust control
Robust control is a branch of control theory that explicitly deals with uncertainty in its approach to controller design. Robust control methods are designed to function properly so long as uncertain parameters or disturbances are within some set...
or adaptive control
Adaptive control
Adaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself...
should be used. A variety of design methods
have been developed by control theorists and control engineers
for both linear and nonlinear systems. Methods of partial control, control by weak signals, etc. have also been developed.
Fields of research and Prospects
Currently an interest in application of control methods in physics is still growing.The following areas of research are being developed actively :
- Control of oscillations
- Control of synchronization
- Control of chaos, bifurcations
- Control of phase transitions, stochastic resonance
- Optimal control in thermodynamics
- Control of micromechanical, molecular and quantum systems
Among most important applications are: control of fusion
Fusion power
Fusion power is the power generated by nuclear fusion processes. In fusion reactions two light atomic nuclei fuse together to form a heavier nucleus . In doing so they release a comparatively large amount of energy arising from the binding energy due to the strong nuclear force which is manifested...
, control of beams, control in nano- and femtotechnologies.
In order to facilitate information exchange in the area of cybernetical physics the International Physics and Control Society (IPACS) was created
The IPACS organizes regular conferences (Physics and Control Conferences), supports electronic library IPACS Electronic Library and information portal Physics and Control Resources.