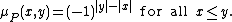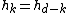In combinatorial

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

 mathematics, an Eulerian poset is a graded poset

Graded poset

In mathematics, in the branch of combinatorics, a graded poset, sometimes called a ranked poset , is a partially ordered set P equipped with a rank function ρ from P to N compatible with the ordering such that whenever y covers x, then...

 in which every nontrivial interval has the same number of elements of even rank as of odd rank. An Eulerian poset which is a lattice

Lattice (order)

In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...

 is an Eulerian lattice. These objects are named after Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

. Eulerian lattices generalize face lattices of convex polytope

Convex polytope

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

s and much recent research has been devoted to extending known results from polyhedral combinatorics

Polyhedral combinatorics

Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytopes....

, such as various restrictions on f-vectors of convex simplicial polytope

Simplicial polytope

In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....

s, to this more general setting.

Examples

• The face lattice of a convex polytope
  Convex polytope
  A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
  
  , consisting of its faces, together with the smallest element, the empty face, and the largest element, the polytope itself, is an Eulerian lattice. The odd–even condition follows from Euler's formula
  Euler characteristic
  In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
  
  .

• Any simplicial generalized homology sphere is an Eulerian lattice.

• Let L be a regular cell complex such that |L| is a manifold
  Manifold
  In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
  
   with the same Euler characteristic as the sphere of the same dimension (this condition is vacuous if the dimension is odd). Then the poset of cells of L, ordered by the inclusion of their closures, is Eulerian.

• Let W be a Coxeter group
  Coxeter group
  In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
  
   with Bruhat order
  Bruhat order
  In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
  
  . Then (W,≤) is an Eulerian poset.

Properties

• The defining condition of an Eulerian poset P can be equivalently stated in terms of its Möbius function
  Incidence algebra
  In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
  
  :

• The dual of an Eulerian poset, obtained by reversing the partial order, is Eulerian.

• Richard Stanley
  Richard P. Stanley
  Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...
  
   defined the toric h-vector of a ranked poset
  Ranked poset
  In mathematics, a ranked partially ordered set - or poset - may be either:* a graded poset, or* a poset that has the property that for every element x, all maximal chains among those with x as greatest element have the same finite length, or...
  
  , which generalizes the h-vector
  H-vector
  In algebraic combinatorics, the h-vector of a simplicial polytope is a fundamental invariant of the polytope which encodes the number of faces of different dimensions and allows one to express the Dehn–Sommerville equations in a particularly simple form...
  
   of a simplicial polytope. He proved that the Dehn–Sommerville equations

hold for an arbitrary Eulerian poset of rank d + 1. However, for an Eulerian poset arising from a regular cell complex or a convex polytope, the toric h-vector neither determines, nor is neither determined by the numbers of the cells or faces of different dimension and the toric h-vector does not have a direct combinatorial interpretation.