Fransén-Robinson constant
Encyclopedia
The Fransén–Robinson constant, sometimes denoted F, is the mathematical constant
that represents the area between the graph of the reciprocal Gamma function,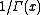
, and the positive x axis. That is,
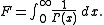
The Fransén–Robinson constant has numerical value F = 2.8077702420285... , with the continued fraction
representation [2; 1, 4, 4, 1, 18, 5, 1, 3, 4, 1, 5, 3, 6, ...] . Its proximity to Euler's number
e = 2.71828... follows from the fact that the integral can be approximated by
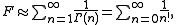
the standard series for e. The difference is given by
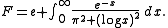
and also by
The Fransén–Robinson constant can also be expressed using the Mittag-Leffler function
as the limit
It is however unknown whether F can be expressed in closed form
in terms of other known constants.
A fair amount of effort has been made to calculate the numerical value of the Fransén–Robinson constant with high accuracy. The value was computed to 36 decimal places by Herman P. Robinson using 11-point Newton–Cotes quadrature, with 65 digits by A. Fransén using Euler–Maclaurin summation, and with 80 digits by Fransén and S. Wrigge using Taylor series
and other methods. William A. Johnson computed 300 digits, and Pascal Sebah was able to compute 600 digits using Clenshaw–Curtis integration.
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
that represents the area between the graph of the reciprocal Gamma function,
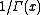, and the positive x axis. That is,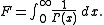The Fransén–Robinson constant has numerical value F = 2.8077702420285... , with the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
representation [2; 1, 4, 4, 1, 18, 5, 1, 3, 4, 1, 5, 3, 6, ...] . Its proximity to Euler's number
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
e = 2.71828... follows from the fact that the integral can be approximated by
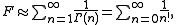
the standard series for e. The difference is given by
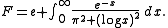
and also by
The Fransén–Robinson constant can also be expressed using the Mittag-Leffler function
Mittag-Leffler function
In mathematics, the Mittag-Leffler function Eα,β is a special function, a complex function which depends on two complex parameters α and β...
as the limit
It is however unknown whether F can be expressed in closed form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
in terms of other known constants.
A fair amount of effort has been made to calculate the numerical value of the Fransén–Robinson constant with high accuracy. The value was computed to 36 decimal places by Herman P. Robinson using 11-point Newton–Cotes quadrature, with 65 digits by A. Fransén using Euler–Maclaurin summation, and with 80 digits by Fransén and S. Wrigge using Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
and other methods. William A. Johnson computed 300 digits, and Pascal Sebah was able to compute 600 digits using Clenshaw–Curtis integration.