Function and Concept
Encyclopedia
"On Function and Concept" (Über Funktion und Begriff) is an article by Gottlob Frege
, published in 1891. The article involves a clarification of his earlier distinction between concepts and objects.
In general, a concept is a function
whose value is always a truth value (139). A relation is a two place function whose value is always a truth value (146).
Frege draws an important distinction between concepts on the basis of their level. Frege tells us that a first-level concept is a one-place function that correlates objects with truth-values (147). First level concepts have the value of true or false depending on whether the object falls under the concept. So, the concept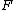
has the value the True with the argument the object named by 'Jamie' if and only if Jamie falls under the concept 
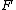(or is in the extension of F).
Second order concepts correlate concepts and relations with truth values. So, if we take the relation of identity to be the argument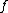
, the concept expressed by the sentence:
correlates the relation of identity with the True.
The conceptual range (Begriffsumfang) follows the truth value of the function:
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
, published in 1891. The article involves a clarification of his earlier distinction between concepts and objects.
In general, a concept is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
whose value is always a truth value (139). A relation is a two place function whose value is always a truth value (146).
Frege draws an important distinction between concepts on the basis of their level. Frege tells us that a first-level concept is a one-place function that correlates objects with truth-values (147). First level concepts have the value of true or false depending on whether the object falls under the concept. So, the concept
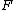has the value the True with the argument the object named by 'Jamie' if and only if Jamie falls under the concept 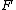(or is in the extension of F).Second order concepts correlate concepts and relations with truth values. So, if we take the relation of identity to be the argument
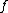, the concept expressed by the sentence:correlates the relation of identity with the True.
The conceptual range (Begriffsumfang) follows the truth value of the function:
- x2 = 1 and (x + 1)2 = 2(x + 1) have the same conceptual range.