
Gradually varied surface
Encyclopedia
In mathematics, a gradually varied surface is a special type of digital surfaces. It is a function from a 2D digital space (see digital geometry
) to an ordered set or a chain.
A gradually varied function is a function from a digital space to
to  where
where  and
and 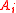 are real numbers. This function possesses the following property: If x and y are two adjacent points in
are real numbers. This function possesses the following property: If x and y are two adjacent points in  , assume
, assume  , then
, then  ,
, 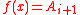 , or
, or  .
.
The concept of the continuous function in digital space (can be called digitally continuous functions) was proposed by Azriel Rosenfeld
in 1986. It is a function in which the value (an integer) at a digital point is the same or almost the same as its neighbors. In other words, if x and y are two adjacent points in a digital space, |f(x) − f(y)| ≤ 1.
So we can see that the gradually varied function is defined to be more general than the digitally continuous function. The gradually varied function was defined by L. Chen in 1989.
An extension theorem related to above functions was mentioned by Rosenfeld (1986) and completed by Chen (1989). This theorem states: Let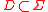 and
and 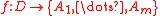 . The necessary and sufficient condition for the existence of the gradually varied extension
. The necessary and sufficient condition for the existence of the gradually varied extension  of
of 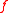 is : for each pair of points
is : for each pair of points  and
and 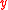 in
in  , assume
, assume  and
and 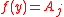 , we have
, we have 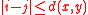 , where
, where 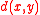 is the (digital) distance between
is the (digital) distance between  and
and  .
.
The gradually varied surface has direct relationship to graph homomorphism
.
Digital geometry
Digital geometry deals with discrete sets considered to be digitized models or images of objects of the 2D or 3D Euclidean space.Simply put, digitizing is replacing an object by a discrete set of its points...
) to an ordered set or a chain.
A gradually varied function is a function from a digital space
 to
to  where
where  and
and 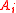 are real numbers. This function possesses the following property: If x and y are two adjacent points in
are real numbers. This function possesses the following property: If x and y are two adjacent points in  , assume
, assume  , then
, then  ,
, 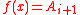 , or
, or  .
.The concept of the continuous function in digital space (can be called digitally continuous functions) was proposed by Azriel Rosenfeld
Azriel Rosenfeld
Professor Dr. Azriel Rosenfeld was an American Research Professor, a Distinguished University Professor, and Director of the Center for Automation Research at the University of Maryland in College Park, Maryland, where he also held affiliate professorships in the Departments of Computer Science,...
in 1986. It is a function in which the value (an integer) at a digital point is the same or almost the same as its neighbors. In other words, if x and y are two adjacent points in a digital space, |f(x) − f(y)| ≤ 1.
So we can see that the gradually varied function is defined to be more general than the digitally continuous function. The gradually varied function was defined by L. Chen in 1989.
An extension theorem related to above functions was mentioned by Rosenfeld (1986) and completed by Chen (1989). This theorem states: Let
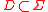 and
and 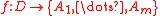 . The necessary and sufficient condition for the existence of the gradually varied extension
. The necessary and sufficient condition for the existence of the gradually varied extension  of
of 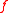 is : for each pair of points
is : for each pair of points  and
and 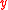 in
in  , assume
, assume  and
and 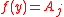 , we have
, we have 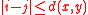 , where
, where 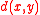 is the (digital) distance between
is the (digital) distance between  and
and  .
.The gradually varied surface has direct relationship to graph homomorphism
Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
.

