Injective sheaf
Encyclopedia
In mathematics
, injective sheaves of abelian group
s are used to construct the resolutions needed to define sheaf cohomology
(and other derived functor
s, such as sheaf Ext
).
There is a further group of related concepts applied to sheaves
: flabby (flasque in French), fine, soft (mou in French), acyclic. In the history of the subject they were introduced before the 1957 'Tohoku' paper of Alexander Grothendieck
, which showed that the abelian category
notion of injective object
sufficed to found the theory. The other classes of sheaves are historically older notions. The abstract framework of defining cohomology and derived functors does not need them. However, in most concrete situations, resolutions by acyclic sheaves are often easier to construct. Acyclic sheaves therefore serve for computational purposes, for example the Leray spectral sequence
.
The category of abelian sheaves has enough injective elements: this means that any sheaf is a subsheaf of an injective sheaf. This result of Grothendieck follows from the existence of a generator of the category (it can be written down explicitly, and is related to the subobject classifier
). This is enough to show that right derived functors of any left exact functor exist and are unique up to canonical isomorphism.
For technical purposes, injective sheaves are usually superior to the other classes of sheaves mentioned above: they can do almost anything the other classes can do, and their theory is simpler and more general. In fact, injective sheaves are flabby (flasque), soft, and acyclic. However, there are situations where the other classes of sheaves occur naturally, and this is especially true in concrete computational situations.
The dual concept, projective sheaves, is not used much, because in a general category of sheaves there are not enough of them: not every sheaf is the quotient of a projective sheaf, and in particular projective resolutions do not always exist. This is the case, for example, when looking at the category of sheaves on projective space
in the Zariski topology. This causes problems when attempting to define left derived functors of a right exact functor (such as Tor). This can sometimes be done by ad hoc means: for example, the left derived functors of Tor can be defined using a flat resolution rather than a projective one, but it takes some work to show that this is independent of the resolution. Not all categories of sheaves run into this problem; for instance, the category of sheaves on an affine scheme contains enough projectives.
The cohomology groups of any sheaf can be calculated from any acyclic resolution of it (this goes by the name of De Rham-Weil theorem
).
Fine sheaves are usually only used over paracompact Hausdorff spaces X. Typical examples are the sheaf of continuous real functions over such a space, or smooth functions over a smooth (paracompact Hausdorff) manifold, or modules over these sheaves of rings.
Fine sheaves over paracompact Hausdorff spaces are soft and acyclic.
As an application, consider a real manifold
X. There is the following resolution of the constant sheaf ℝ by the fine sheaves of (smooth) differential forms:
This is a resolution, i.e. an exact complex of sheaves by the Poincaré lemma. The cohomology of X with values in ℝ can thus be computed as the cohomology of the complex of globally defined differential forms:
subset of X can be extended to a global section.
Soft sheaves are acyclic over paracompact Hausdorff spaces.
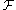with the following property: if 
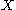is the base topological space
on which the sheaf is defined and
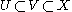
are open subsets, then the restriction map
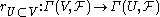
is surjective, as a map of groups
(rings
, modules
, etc.).
Flasque sheaves are useful because (by definition) sections of them extend. This means that they are some of the simplest sheaves to handle in terms of homological algebra
.
Any sheaf has a canonical embedding into the flasque sheaf of all possibly discontinuous sections of the étalé space, and by repeating this we can find a canonical flasque resolution for any sheaf.
Flasque resolutions, that is, resolutions by means of flasque sheaves, are one approach to defining sheaf cohomology
.
Flasque is a French
word, that has sometimes been translated into English as flabby.
Flasque sheaves are soft and acyclic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, injective sheaves of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s are used to construct the resolutions needed to define sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
(and other derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s, such as sheaf Ext
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
).
There is a further group of related concepts applied to sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
: flabby (flasque in French), fine, soft (mou in French), acyclic. In the history of the subject they were introduced before the 1957 'Tohoku' paper of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, which showed that the abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
notion of injective object
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
sufficed to found the theory. The other classes of sheaves are historically older notions. The abstract framework of defining cohomology and derived functors does not need them. However, in most concrete situations, resolutions by acyclic sheaves are often easier to construct. Acyclic sheaves therefore serve for computational purposes, for example the Leray spectral sequence
Leray spectral sequence
In mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. The formulation was of a spectral sequence, expressing the relationship holding in sheaf cohomology between two topological spaces X and Y, and set up by a continuous...
.
Injective sheaves
An injective sheaf F is just a sheaf that is an injective element of the category of abelian sheaves; in other words, homomorphisms from A to F can always be lifted to any sheaf B containing A.The category of abelian sheaves has enough injective elements: this means that any sheaf is a subsheaf of an injective sheaf. This result of Grothendieck follows from the existence of a generator of the category (it can be written down explicitly, and is related to the subobject classifier
Subobject classifier
In category theory, a subobject classifier is a special object Ω of a category; intuitively, the subobjects of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements...
). This is enough to show that right derived functors of any left exact functor exist and are unique up to canonical isomorphism.
For technical purposes, injective sheaves are usually superior to the other classes of sheaves mentioned above: they can do almost anything the other classes can do, and their theory is simpler and more general. In fact, injective sheaves are flabby (flasque), soft, and acyclic. However, there are situations where the other classes of sheaves occur naturally, and this is especially true in concrete computational situations.
The dual concept, projective sheaves, is not used much, because in a general category of sheaves there are not enough of them: not every sheaf is the quotient of a projective sheaf, and in particular projective resolutions do not always exist. This is the case, for example, when looking at the category of sheaves on projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
in the Zariski topology. This causes problems when attempting to define left derived functors of a right exact functor (such as Tor). This can sometimes be done by ad hoc means: for example, the left derived functors of Tor can be defined using a flat resolution rather than a projective one, but it takes some work to show that this is independent of the resolution. Not all categories of sheaves run into this problem; for instance, the category of sheaves on an affine scheme contains enough projectives.
Acyclic sheaves
An acyclic sheaf F over X is one such that all higher sheaf cohomology groups vanish.The cohomology groups of any sheaf can be calculated from any acyclic resolution of it (this goes by the name of De Rham-Weil theorem
De Rham-Weil theorem
In algebraic topology, the De Rham-Weil theorem allows computation of sheaf cohomology using an acyclic resolution of the sheaf in question.Let \mathcal F be a sheaf on a topological space X and \mathcal F^\bullet a resolution of \mathcal F by acyclic sheaves...
).
Fine sheaves
A fine sheaf over X is one with "partitions of unity"; more precisely for any open cover of the space X we can find a family of homomorphisms from the sheaf to itself with sum 1 such that each homomorphism is 0 outside some element of the open cover.Fine sheaves are usually only used over paracompact Hausdorff spaces X. Typical examples are the sheaf of continuous real functions over such a space, or smooth functions over a smooth (paracompact Hausdorff) manifold, or modules over these sheaves of rings.
Fine sheaves over paracompact Hausdorff spaces are soft and acyclic.
As an application, consider a real manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
X. There is the following resolution of the constant sheaf ℝ by the fine sheaves of (smooth) differential forms:
- 0 → ℝ → C0X → C1X → ... → Cdim XX → 0
This is a resolution, i.e. an exact complex of sheaves by the Poincaré lemma. The cohomology of X with values in ℝ can thus be computed as the cohomology of the complex of globally defined differential forms:
- Hi(X, ℝ) = Hi(C·X(X)).
Soft sheaves
A soft sheaf F over X is one such that any section over any closedsubset of X can be extended to a global section.
Soft sheaves are acyclic over paracompact Hausdorff spaces.
Flasque or flabby sheaves
A flasque sheaf (also called a flabby sheaf) is a sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
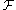with the following property: if 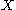is the base topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
on which the sheaf is defined and
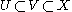
are open subsets, then the restriction map
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
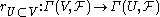
is surjective, as a map of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, etc.).
Flasque sheaves are useful because (by definition) sections of them extend. This means that they are some of the simplest sheaves to handle in terms of homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
.
Any sheaf has a canonical embedding into the flasque sheaf of all possibly discontinuous sections of the étalé space, and by repeating this we can find a canonical flasque resolution for any sheaf.
Flasque resolutions, that is, resolutions by means of flasque sheaves, are one approach to defining sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
.
Flasque is a French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
word, that has sometimes been translated into English as flabby.
Flasque sheaves are soft and acyclic.