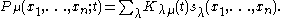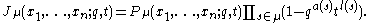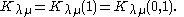Kostka polynomial
Encyclopedia
In mathematics, a Kostka polynomial or Kostka–Foulkes polynomial Kλμ(q, t), named after Carl Kostka
, is a polynomial in two variables with non-negative integer coefficients depending on two partition
s λ and μ. Sometimes the variable q is fixed to be 0 in which case the polynomials are denoted by Kλμ(t) = Kλμ(0,t).
The two-variable polynomials are also called Macdonald–Kostka polynomials or q,t-Kostka polynomials. There are two slightly different versions of them, one called transformed Kostka polynomials.
The one variable polynomials can be used to express Hall-Littlewood polynomials Pμ as a linear combination of Schur polynomial
s sλ:
The Macdonald–Kostka polynomials can be used to express Macdonald polynomial
s (also denoted by) Pμ as a linear combination of Schur polynomial
s sλ:
where
Kostka number
s are special values of the 1 or 2 variable Kostka polynomials:
Carl Kostka
Carl Kostka was a mathematician who introduced Kostka numbers in 1882. He lived and worked in Insterburg.-References:...
, is a polynomial in two variables with non-negative integer coefficients depending on two partition
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
s λ and μ. Sometimes the variable q is fixed to be 0 in which case the polynomials are denoted by Kλμ(t) = Kλμ(0,t).
The two-variable polynomials are also called Macdonald–Kostka polynomials or q,t-Kostka polynomials. There are two slightly different versions of them, one called transformed Kostka polynomials.
The one variable polynomials can be used to express Hall-Littlewood polynomials Pμ as a linear combination of Schur polynomial
Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
s sλ:
The Macdonald–Kostka polynomials can be used to express Macdonald polynomial
Macdonald polynomial
In mathematics, Macdonald polynomials Pλ are a family of orthogonal polynomials in several variables, introduced by...
s (also denoted by) Pμ as a linear combination of Schur polynomial
Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
s sλ:
where
Kostka number
Kostka number
In mathematics, a Kostka number Kλμ, introduced by , is a non-negative integer depending on two partitions λ and μ, that is equal to the number of semistandard Young tableaux of shape λ and weight μ....
s are special values of the 1 or 2 variable Kostka polynomials: