
Lacunary function
Encyclopedia
In analysis
, a lacunary function, also known as a lacunary series, is an analytic function
that cannot be analytically continued
anywhere outside the radius of convergence
within which it is defined by a power series. The word lacunary is derived from lacuna (pl. lacunae), meaning gap, or vacancy.
The first known examples of lacunary functions involved Taylor series
with large gaps, or lacunae, between the non-zero coefficients of their expansions. More recent investigations have also focused attention on Fourier series
with similar gaps between non-zero coefficients. There is a slight ambiguity in the modern usage of the term lacunary series, which may be used to refer to either Taylor series or Fourier series.
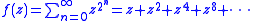
The power series clearly converges uniformly on any open domain |z| < 1, by comparison with the familiar geometric series, which is absolutely convergent when |z| < 1. So f is analytic on the open unit disk. Nevertheless f has a singularity at every point on the unit circle, and cannot be analytically continued outside of the open unit disk, as the following argument demonstrates.
Clearly f has a singularity at z = 1, because
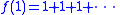
is a divergent series. But since
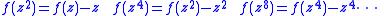
we can see that f has a singularity at a point z when z2 = 1 (that is, when z = ±1), and also when z4 = 1 (that is, when z = ±1 or when z = ±i). By the induction suggested by the above equations, f must have a singularity at each of the 2nth roots of unity
for all natural numbers n. The set of all such points is dense
on the unit circle, hence by continuous extension every point on the unit circle must be a singularity of f.
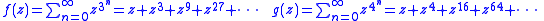
also define lacunary functions. What is not so evident is that the gaps between the powers of z can expand much more slowly, and the resulting series will still define a lacunary function. To make this notion more precise some additional notation is needed.
We write
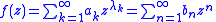
where bn = ak when n = λk, and bn = 0 otherwise. The stretches where the coefficients bn in the second series are all zero are the lacunae in the coefficients. The monotonically increasing sequence of positive natural numbers {λk} specifies the powers of z which are in the power series for f(z).
Now a theorem of Hadamard can be stated. If
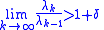
where δ > 0 is an arbitrary positive constant, then f(z) is a lacunary function that cannot be continued outside its circle of convergence. In other words, the sequence {λk} doesn't have to grow as fast as 2k for f(z) to be a lacunary function – it just has to grow as fast as some geometric progression (1 + δ)k. A series for which λk grows this quickly is said to contain Hadamard gaps. See Ostrowski-Hadamard gap theorem.
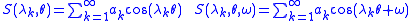
for which the λk are far apart. Here the coefficients ak are real numbers. In this context, attention has been focused on criteria sufficient to guarantee convergence of the trigonometric series almost everywhere
(that is, for almost every value of the angle θ and of the distortion factor ω).
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a lacunary function, also known as a lacunary series, is an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
that cannot be analytically continued
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
anywhere outside the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
within which it is defined by a power series. The word lacunary is derived from lacuna (pl. lacunae), meaning gap, or vacancy.
The first known examples of lacunary functions involved Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
with large gaps, or lacunae, between the non-zero coefficients of their expansions. More recent investigations have also focused attention on Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
with similar gaps between non-zero coefficients. There is a slight ambiguity in the modern usage of the term lacunary series, which may be used to refer to either Taylor series or Fourier series.
A simple example
Consider the lacunary function defined by a simple power series: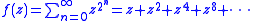
The power series clearly converges uniformly on any open domain |z| < 1, by comparison with the familiar geometric series, which is absolutely convergent when |z| < 1. So f is analytic on the open unit disk. Nevertheless f has a singularity at every point on the unit circle, and cannot be analytically continued outside of the open unit disk, as the following argument demonstrates.
Clearly f has a singularity at z = 1, because
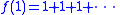
is a divergent series. But since
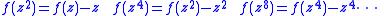
we can see that f has a singularity at a point z when z2 = 1 (that is, when z = ±1), and also when z4 = 1 (that is, when z = ±1 or when z = ±i). By the induction suggested by the above equations, f must have a singularity at each of the 2nth roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
for all natural numbers n. The set of all such points is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
on the unit circle, hence by continuous extension every point on the unit circle must be a singularity of f.
An elementary result
Evidently the argument advanced in the simple example can also be applied to show that series like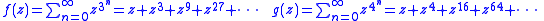
also define lacunary functions. What is not so evident is that the gaps between the powers of z can expand much more slowly, and the resulting series will still define a lacunary function. To make this notion more precise some additional notation is needed.
We write
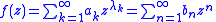
where bn = ak when n = λk, and bn = 0 otherwise. The stretches where the coefficients bn in the second series are all zero are the lacunae in the coefficients. The monotonically increasing sequence of positive natural numbers {λk} specifies the powers of z which are in the power series for f(z).
Now a theorem of Hadamard can be stated. If
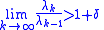
where δ > 0 is an arbitrary positive constant, then f(z) is a lacunary function that cannot be continued outside its circle of convergence. In other words, the sequence {λk} doesn't have to grow as fast as 2k for f(z) to be a lacunary function – it just has to grow as fast as some geometric progression (1 + δ)k. A series for which λk grows this quickly is said to contain Hadamard gaps. See Ostrowski-Hadamard gap theorem.
Lacunary trigonometric series
Mathematicians have also investigated the properties of lacunary trigonometric series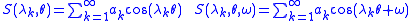
for which the λk are far apart. Here the coefficients ak are real numbers. In this context, attention has been focused on criteria sufficient to guarantee convergence of the trigonometric series almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
(that is, for almost every value of the angle θ and of the distortion factor ω).
- KolmogorovAndrey KolmogorovAndrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
showed that if the sequence {λk} contains Hadamard gaps, then the series S(λk, θ, ω) converges (diverges) almost everywhere when
-
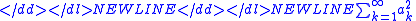
- converges (diverges).
- ZygmundAntoni ZygmundAntoni Zygmund was a Polish-born American mathematician.-Life:Born in Warsaw, Zygmund obtained his PhD from Warsaw University and became a professor at Stefan Batory University at Wilno...
showed under the same condition that S(λk, θ, ω) is not a Fourier series representing an integrable function when this sum of squares of the ak is a divergent series.
- Zygmund
A unified view
Greater insight into the underlying question that motivates the investigation of lacunary power series and lacunary trigonometric series can be gained by re-examining the simple example above. In that example we used the geometric series
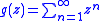
and the Weierstrass M-test to demonstrate that the simple example defines an analytic function on the open unit disk.
The geometric series itself defines an analytic function that converges everywhere on the closed unit disk except when z = 1, where g(z) has a simple pole. And, since z = eiθ for points on the unit circle, the geometric series becomes
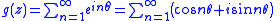
at a particular z, |z| = 1. From this perspective, then, mathematicians who investigate lacunary series are asking the question: How much does the geometric series have to be distorted – by chopping big sections out, and by introducing coefficients ak ≠ 1 – before the resulting mathematical object is transformed from a nice smooth meromorphic functionMeromorphic functionIn complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
into something that exhibits a primitive form of chaoticChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
behavior?
See also
- Analytic continuationAnalytic continuationIn complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
- Szolem Mandelbrojt
- Benoit MandelbrotBenoît MandelbrotBenoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
- Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
External links
- Fukuyama and Takahashi, 1999 A paper (PDF) entitled The Central Limit Theorem for Lacunary Series, from the AMS.
- Mandelbrojt and Miles, 1927 A paper (PDF) entitled Lacunary Functions, from Rice University.
- MathWorld article on Lacunary Functions
- converges (diverges).

