Lemaitre metric
Encyclopedia
Lemaître coordinates are a particular set of coordinates for the Schwarzschild metric
—a spherically symmetric solution to vacuum Einstein equation— obtained by Georges Lemaître
in 1938. Changing to Lemaître coordinates removes the coordinate singularity at the Schwarzschild radius
, which is present in Schwarzschild coordinates
.
, is given as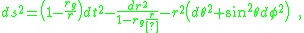
where
is the invariant interval
;
is the gravitational radius;
is the mass of the central body;
are the Schwarzschild coordinates
(which asymptotically turn into the flat spherical coordinates);
is the speed of light
;
This metric has a coordinate singularity at the gravitational radius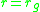
.
Georges Lemaître was the first to show that this is not a real physical singularity but simply a manifestation of the fact that the static Schwarzschild coordinates cannot be realized with material bodies inside the gravitational radius. Indeed inside the gravitational radius everything falls towards the centre and it is impossible for a physical body to keep a constant radius.
A transformation of the Schwarzschild coordinate system from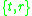
to the new coordinates 
,
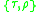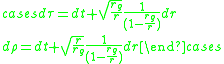
(notice that the numerator and denominator are switched inside the square-roots),
leads to the Lemaître coordinate expression of the metric,
where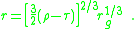
In Lemaître coordinates there is no singularity at the gravitational radius, which instead corresponds to the point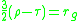
. However, there remains a genuine gravitational singularity
at the centrum, where
, which cannot be removed by a coordinate change.
The Lemaître coordinate system is synchronous, that is, the global time coordinate of the metric defines the proper time of co-moving observers. The radially falling bodies reach the gravitational radius and the centre within finite proper time.
Along the tragectory of a radial light ray,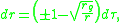
therefore no signal can escape from inside the Schwarzschild radius, where always
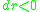and the light rays emitted radially inwards and outwards both
end up at the origin.
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
—a spherically symmetric solution to vacuum Einstein equation— obtained by Georges Lemaître
Georges Lemaître
Monsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...
in 1938. Changing to Lemaître coordinates removes the coordinate singularity at the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
, which is present in Schwarzschild coordinates
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
.
The Lemaître coordinates
The original Schwarzschild coordinate expression of the Schwarzschild metric, in natural unitsNatural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
, is given as
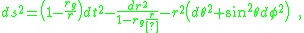
where
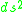is the invariant intervalInvariant interval
In physics, the invariant interval is the measure of separation between two arbitrarily close events in the spacetime of general or special theory of relativity. It is invariant under the coordinate transformations from the covariance group of the theory...
;
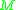is the gravitational radius; is the mass of the central body; are the Schwarzschild coordinatesSchwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
(which asymptotically turn into the flat spherical coordinates);
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
;
- and
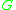is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
.
This metric has a coordinate singularity at the gravitational radius
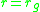.Georges Lemaître was the first to show that this is not a real physical singularity but simply a manifestation of the fact that the static Schwarzschild coordinates cannot be realized with material bodies inside the gravitational radius. Indeed inside the gravitational radius everything falls towards the centre and it is impossible for a physical body to keep a constant radius.
A transformation of the Schwarzschild coordinate system from
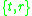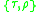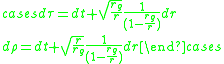
to the new coordinates ,(notice that the numerator and denominator are switched inside the square-roots),
leads to the Lemaître coordinate expression of the metric,
where
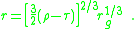
In Lemaître coordinates there is no singularity at the gravitational radius, which instead corresponds to the point
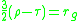. However, there remains a genuine gravitational singularityGravitational singularity
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system...
at the centrum, where
, which cannot be removed by a coordinate change.The Lemaître coordinate system is synchronous, that is, the global time coordinate of the metric defines the proper time of co-moving observers. The radially falling bodies reach the gravitational radius and the centre within finite proper time.
Along the tragectory of a radial light ray,
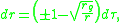
therefore no signal can escape from inside the Schwarzschild radius, where always
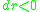and the light rays emitted radially inwards and outwards bothend up at the origin.