
Linear span
Encyclopedia
In the mathematical
subfield of linear algebra
, the linear span (also called the linear hull) of a set of vectors
in a vector space
is the intersection
of all subspaces
containing that set. The linear span of a set of vectors is therefore a vector space.
V over a field
K, the span of a set S (not necessarily finite) is defined to be the intersection W of all subspaces
of V which contain S. W is referred to as the subspace spanned by S, or by the vectors in S. Conversely, S is called a spanning set of W
If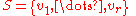 is a finite subset of V, then the span is
is a finite subset of V, then the span is
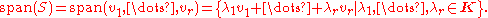
The span of S may also be defined as the set of all linear combinations of the elements of S, which follows from the above definition.
is called a spanning set if the rank of X equals the rank of the entire ground set.
vector space R3 has {(2,0,0), (0,1,0), (0,0,1)} as a spanning set. This particular spanning set is also a basis
. If (2,0,0) were replaced by (1,0,0), it would also form the canonical basis
of R3.
Another spanning set for the same space is given by {(1,2,3), (0,1,2), (−1,1/2,3), (1,1,1)}, but this set is not a basis, because it is linearly dependent.
The set {(1,0,0), (0,1,0), (1,1,0)} is not a spanning set of R3; instead its span is the space of all vectors in R3 whose last component is zero.
This theorem is so well known that at times it is referred to as the definition of span of a set.
Theorem 2: Every spanning set S of a vector space V must contain at least as many elements as any linearly independent
set of vectors from V.
Theorem 3: Let V be a finite dimensional vector space. Any set of vectors that spans V can be reduced to a basis for V by discarding vectors if necessary (i.e. if there are linearly dependent vectors in the set). If the axiom of choice holds, this is true without the assumption that V has finite dimension.
This also indicates that a basis is a minimal spanning set when V is finite dimensional.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subfield of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the linear span (also called the linear hull) of a set of vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
in a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of all subspaces
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
containing that set. The linear span of a set of vectors is therefore a vector space.
Definition
Given a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, the span of a set S (not necessarily finite) is defined to be the intersection W of all subspaces
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of V which contain S. W is referred to as the subspace spanned by S, or by the vectors in S. Conversely, S is called a spanning set of W
If
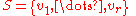 is a finite subset of V, then the span is
is a finite subset of V, then the span is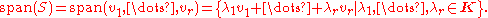
The span of S may also be defined as the set of all linear combinations of the elements of S, which follows from the above definition.
Matroids
Generalizing the definition of the span of points in space, a subset X of the ground set of a matroidMatroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
is called a spanning set if the rank of X equals the rank of the entire ground set.
Examples
The realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space R3 has {(2,0,0), (0,1,0), (0,0,1)} as a spanning set. This particular spanning set is also a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
. If (2,0,0) were replaced by (1,0,0), it would also form the canonical basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
of R3.
Another spanning set for the same space is given by {(1,2,3), (0,1,2), (−1,1/2,3), (1,1,1)}, but this set is not a basis, because it is linearly dependent.
The set {(1,0,0), (0,1,0), (1,1,0)} is not a spanning set of R3; instead its span is the space of all vectors in R3 whose last component is zero.
Theorems
Theorem 1: The subspace spanned by a non-empty subset S of a vector space V is the set of all linear combinations of vectors in S.This theorem is so well known that at times it is referred to as the definition of span of a set.
Theorem 2: Every spanning set S of a vector space V must contain at least as many elements as any linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
set of vectors from V.
Theorem 3: Let V be a finite dimensional vector space. Any set of vectors that spans V can be reduced to a basis for V by discarding vectors if necessary (i.e. if there are linearly dependent vectors in the set). If the axiom of choice holds, this is true without the assumption that V has finite dimension.
This also indicates that a basis is a minimal spanning set when V is finite dimensional.

