Liénard's theorem
Encyclopedia
In mathematics
, more specifically in the study of dynamical system
s and differential equation
s, a Liénard equation is a second order differential equation, named after the French physicist Alfred-Marie Liénard
.
During the development of radio
and vacuum tube
technology, Liénard equations were intensely studied as they can be used to model oscillating circuits. Under certain additional assumptions Liénard's theorem guarantees the uniqueness and existence of a limit cycle for such a system.
of the form
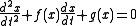
is called the Liénard equation.
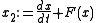
then
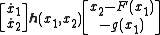
is called a Liénard system.
Alternatively, since Liénard equation itself also belongs to autonomous differential equation, the substitution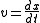
leads the Liénard equation to a first order differential equation:
which belongs to Abel equation of the second kind.
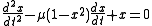
is a Liénard equation.
limit cycle surrounding the origin if it satisfies the following additional properties:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in the study of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s and differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, a Liénard equation is a second order differential equation, named after the French physicist Alfred-Marie Liénard
Alfred-Marie Liénard
Alfred-Marie Liénard , was a French physicist and engineer. He is most well known for his invention of the Liénard–Wiechert potentials....
.
During the development of radio
Radio
Radio is the transmission of signals through free space by modulation of electromagnetic waves with frequencies below those of visible light. Electromagnetic radiation travels by means of oscillating electromagnetic fields that pass through the air and the vacuum of space...
and vacuum tube
Vacuum tube
In electronics, a vacuum tube, electron tube , or thermionic valve , reduced to simply "tube" or "valve" in everyday parlance, is a device that relies on the flow of electric current through a vacuum...
technology, Liénard equations were intensely studied as they can be used to model oscillating circuits. Under certain additional assumptions Liénard's theorem guarantees the uniqueness and existence of a limit cycle for such a system.
Definition
Let f and g be two continuously differentiable functions on R, with g an odd function and f an even function then the second order ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
of the form
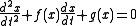
is called the Liénard equation.
Liénard system
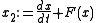
The equation can be transformed into an equivalent two-dimensional system of ordinary differential equations. We definethen
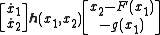
is called a Liénard system.
Alternatively, since Liénard equation itself also belongs to autonomous differential equation, the substitution
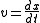leads the Liénard equation to a first order differential equation:which belongs to Abel equation of the second kind.
Example
The Van der Pol oscillator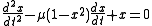is a Liénard equation.
Liénard's theorem
A Liénard system has a unique and stableStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
limit cycle surrounding the origin if it satisfies the following additional properties:
- g(x) > 0 for all x > 0;
-
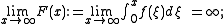
- F(x) has exactly one positive root at some value p, where F(x) < 0 for 0 < x < p and F(x) > 0 and monotonic for x > p.