
Multiple-scale analysis
Encyclopedia
In mathematics
and physics
, multiple-scale analysis (also called the method of multiple scales) comprises techniques used to construct uniformly valid approximation
s to the solutions of perturbation problems
, both for small as well as large values of the independent variable
s. This is done by introducing fast-scale and slow-scale variables for an independent variable, and subsequently treating these variables, fast and slow, as if they are independent. In the solution process of the perturbation problem thereafter, the resulting additional freedom – introduced by the new independent variables – is used to remove (unwanted) secular terms
. The latter puts constraints on the approximate solution, which are called solvability conditions.
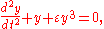
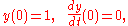
which is a second-order ordinary differential equation
describing a nonlinear oscillator. A solution y(t) is sought for small values of the (positive) nonlinearity parameter 0 < ε ≪ 1. The undamped Duffing equation is known to be a Hamiltonian system
:

with q = y(t) and p = dy/dt. Consequently, the Hamiltonian H(p, q) is a conserved quantity, a constant, equal to H = ½ + ¼ ε for the given initial conditions. This implies that both y and dy/dt have to be bounded:

to the problem gives the result:
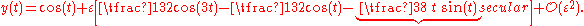
The last term between the square braces is secular: it grows without bound for large |t|, making the perturbation solution valid for only small values of the time t.

and assume the solution y(t) is a perturbation-series solution dependent both on t and t1, treated as:

So:
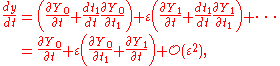
using dt1/dt = ε. Similarly:
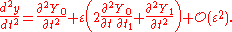
Then the zeroth- and first-order problems of the multiple-scales perturbation series for the Duffing equation become:
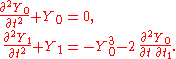
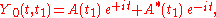
with A(t1) a complex-valued
amplitude
to the zeroth-order solution Y0(t, t1) and i2 = −1. Now, in the first-order problem the forcing in the right hand side of the differential equation is
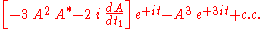
where c.c. denotes the complex conjugate
of the preceding terms. The occurrence of secular terms can be prevented by imposing on the – yet unknown – amplitude A(t1) the solvability condition

The solution to the solvability condition, also satisfying the initial conditions y(0) = 1 and dy/dt(0) = 0, is:
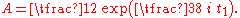
As a result, the approximate solution by the multiple-scales analysis is

using t1 = εt and valid for εt = O(1). This agrees with the nonlinear frequency
changes found by employing the Lindstedt–Poincaré method.
Higher-order solutions – using the method of multiple scales – require the introduction of additional slow scales, i.e.: t2 = ε2 t, t3 = ε3 t, etc. However, this introduces possible ambiguities in the perturbation series solution, which require a careful treatment (see ; ).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, multiple-scale analysis (also called the method of multiple scales) comprises techniques used to construct uniformly valid approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
s to the solutions of perturbation problems
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, both for small as well as large values of the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s. This is done by introducing fast-scale and slow-scale variables for an independent variable, and subsequently treating these variables, fast and slow, as if they are independent. In the solution process of the perturbation problem thereafter, the resulting additional freedom – introduced by the new independent variables – is used to remove (unwanted) secular terms
Secular variation
The secular variation of a time series is its long-term non-periodic variation . Whether something is perceived as a secular variation or not depends on the available timescale: a secular variation over a time scale of centuries may be part of a periodic variation over a time scale of millions of...
. The latter puts constraints on the approximate solution, which are called solvability conditions.
Differential equation and energy conservation
As an example for the method of multiple-scale analysis, consider the undamped and unforced Duffing equation: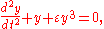
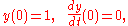
which is a second-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
describing a nonlinear oscillator. A solution y(t) is sought for small values of the (positive) nonlinearity parameter 0 < ε ≪ 1. The undamped Duffing equation is known to be a Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
:

with q = y(t) and p = dy/dt. Consequently, the Hamiltonian H(p, q) is a conserved quantity, a constant, equal to H = ½ + ¼ ε for the given initial conditions. This implies that both y and dy/dt have to be bounded:

Straightforward perturbation-series solution
A regular perturbation-series approachPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
to the problem gives the result:
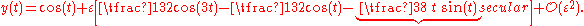
The last term between the square braces is secular: it grows without bound for large |t|, making the perturbation solution valid for only small values of the time t.
Method of multiple scales
To construct a global valid solution, the method of multiple-scale analysis is used. Introduce the slow scale t1:
and assume the solution y(t) is a perturbation-series solution dependent both on t and t1, treated as:

So:
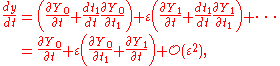
using dt1/dt = ε. Similarly:
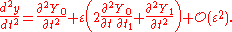
Then the zeroth- and first-order problems of the multiple-scales perturbation series for the Duffing equation become:
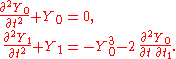
Solution
The zeroth-order problem has the general solution: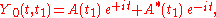
with A(t1) a complex-valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
to the zeroth-order solution Y0(t, t1) and i2 = −1. Now, in the first-order problem the forcing in the right hand side of the differential equation is
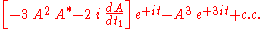
where c.c. denotes the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of the preceding terms. The occurrence of secular terms can be prevented by imposing on the – yet unknown – amplitude A(t1) the solvability condition

The solution to the solvability condition, also satisfying the initial conditions y(0) = 1 and dy/dt(0) = 0, is:
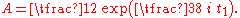
As a result, the approximate solution by the multiple-scales analysis is

using t1 = εt and valid for εt = O(1). This agrees with the nonlinear frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
changes found by employing the Lindstedt–Poincaré method.
Higher-order solutions – using the method of multiple scales – require the introduction of additional slow scales, i.e.: t2 = ε2 t, t3 = ε3 t, etc. However, this introduces possible ambiguities in the perturbation series solution, which require a careful treatment (see ; ).

