
Near sets
Encyclopedia
Near sets are disjoint sets that resemble each other. Resemblance between disjoint sets occurs whenever there are observable similarities between the objects in the sets. Similarity is determined by comparing lists of object feature values. Each list of feature values defines an object's description. Comparison of object descriptions provides a basis for determining the extent that disjoint sets resemble each other. Objects that are perceived as similar based on their descriptions are grouped together. These groups of similar objects can provide information and reveal patterns about objects of interest in the disjoint sets. For example, collections of digital images viewed as disjoint sets of points provide a rich hunting ground for near sets.
Near set theory provides methods that can be used to extract resemblance information from objects contained in disjoint sets, i.e., it provides a formal basis for the observation, comparison, and classification of objects. The discovery of near sets begins with choosing the appropriate method to describe observed objects. This is accomplished by the selection of probe functions representing observable object features. A probe function is a mapping from an object to a real number representing a feature value. For example, when comparing fruit such as apples, the redness of an apple (observed object) can be described by a probe function representing colour, and the output of the probe function is a number representing the degree of redness (or whatever colour apple you prefer to eat). Probe functions provide a basis for describing and discerning affinities between objects as well as between groups of similar objects. Objects that have, in some degree, affinities are considered near each other. Similarly, groups of objects (i.e. sets) that have, in some degree, affinities are also considered near each other.
Near sets offer a framework for solving problems based on human perception
that arise in areas such as image processing
, computer vision
as well as engineering and science problems. In near set theory, perception is a combination of the view of perception in psychophysics
with a view of perception found in Merleau-Ponty's
work. In the context of psychophysics, perception of an object (i.e., in effect, knowledge about an object) depends on signal values gathered by our senses. In this view of perception, our senses are likened to probe functions by considering them as mappings of stimuli to sensations that are a source of values assimilated by the mind. A human sense modelled as a probe measures observable physical characteristics of objects in our environment. The sensed physical characteristics of an object are identified with object features. In Merleau-Ponty's view, an object is perceived to the extent that it can be described. In other words, object description goes hand-in-hand with object perception. It is the mind that identifies relationships between object descriptions to form perceptions of sensed objects. It is also the case that near set theory has been proven to be quite successful in finding solutions to perceptual problems such as measuring image correspondence and segmentation evaluation.

Excitement grew after 2002, when it became apparent that it was possible to introduce measures of nearness based on similarities between classes contained in coverings of disjoint sets (e.g., this is possible if we define coverings of sets representing digital images and then look for similarities between the images such as shades of green in one landscape that resemble one or more shades of green in another landscape). In this context the term similarity
means resemblance between two or more individual objects or sets of objects and almost equal patterns in compared items. Collaboration between J.F. Peters, A. Skowron, and J. Stepaniuk led to a formal basis for the nearness of objects considered in the context of proximity spaces
. Near sets and an approach to defining resemblance between sets was introduced by J.F. Peters in.
Near set theory and its applications grew out of a generalization of the approach to the classification of objects proposed by Z. Pawlak during his work on rough sets
in the early 1980s, and E. Orłowska's work on approximation spaces. Briefly, a rough set can be described as follows. Consider a non-empty finite set of objects labelled . The set
. The set  can be partitioned
can be partitioned
into cells (referred to as classes in near set theory) by grouping together objects that have similar descriptions (using one or more probe functions). A set is considered rough when it cannot be formed completely by the union of classes from the partition of
is considered rough when it cannot be formed completely by the union of classes from the partition of  . The set
. The set  is considered rough inasmuch as
is considered rough inasmuch as  cannot be fully described by probe functions selected to describe the individual objects of
cannot be fully described by probe functions selected to describe the individual objects of  .
.
Near sets are considered a generalization of rough sets, since it has been shown that every rough set is a near set but not every near set is a rough set. Near sets grew out of the idea that two or more rough sets can share objects with matching descriptions if they both contain objects belonging to the same class from the partition of . When this occurs, the sets are considered near each other with respect to the classes contained in the partition.
. When this occurs, the sets are considered near each other with respect to the classes contained in the partition.
An object is anything that has its origin in the physical world.
An identifying characteristic of an object is that it must have some quantifiable features. The term feature is used in S. Watanabe's sense of the word, i.e., a feature corresponds to an observable property of physical objects. Each feature has a 1-to-many relationship to real-valued functions called probe functions representing the feature. For each feature (such as colour) one or more probe functions can be introduced to represent the feature (such as grayscale
, or RGB
values). Objects and sets of probe functions form the basis of near set theory and are sometimes referred to as perceptual objects due to the focus on assigning values to perceived object features. A non-empty, finite set of objects is denoted by .
.
Definition 2: Probe Function
A probe function is a real-valued function, , representing a feature of an object.
, representing a feature of an object.
Examples of probe functions are the colour, size, texture, edge-orientation, or weight of an object. Probe functions are used to describe an object to determine the characteristics and perceptual similarity of objects. Perceptual information is always presented with respect to probe functions just as our senses define our perception of the world. For example, our ability to view light in the visible spectrumrather than infra red or microwaves spectra defines our perception of the world just as the selection of probe functions constrains the amount of perceptual information available for feature extraction from a set of objects. The set of all probe functions is denoted by , and a set of specific probe functions for a given application is denoted by
, and a set of specific probe functions for a given application is denoted by 
Definition 3: Perceptual System
A perceptual system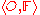 consists of a non-empty set
consists of a non-empty set  together with a set
together with a set  of real-valued functions.
of real-valued functions.
The notion of a perceptual system admits a wide variety of different interpretations that result from the selection of sample objects contained in a particular sample space . A recent example of a perceptual system is given by D. Hall. Two other examples of perceptual systems are: a set of microscope images together with a set of image processing probe functions, or a set of results from a web query together with some measures (probe functions) indicating, e.g., relevancy of the results.
. A recent example of a perceptual system is given by D. Hall. Two other examples of perceptual systems are: a set of microscope images together with a set of image processing probe functions, or a set of results from a web query together with some measures (probe functions) indicating, e.g., relevancy of the results.
Definition 4: Object Description
Consider a perceptual system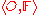 . The description of an object
. The description of an object 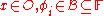 is given by the vector
is given by the vector
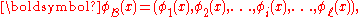
where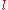 is the length of the vector
is the length of the vector  , and each
, and each 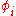 is a probe function belonging to the set
is a probe function belonging to the set 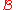 .
.
Definition 5: Perceptual Indiscernibility Relation
Let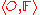 be a perceptual system. For every
be a perceptual system. For every  the perceptual indiscernibility relation
the perceptual indiscernibility relation 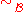 is defined as follows:
is defined as follows:
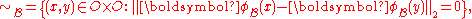
where represents the
represents the 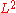 norm
norm
. This is a refinement of the original indiscernibility relation given by Pawlak in 1981. Using the perceptual indiscernibility relation, objects with matching descriptions can be grouped to form classes called elementary sets (also called an equivalence class) defined by
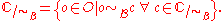
Similarly, a quotient set is the set of all elementary sets defined as
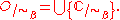
Definition 6: Perceptual Tolerance Relation
When dealing with perceptual objects (especially, components in images), it is sometimes necessary to relax the equivalence condition of Defn. 5 to facilitate observation of associations in a perceptual system. This variation is called a perceptual tolerance relation. Let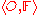 be a perceptual system and let
be a perceptual system and let 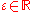 . For every
. For every the tolerance relation
the tolerance relation  is defined as follows:
is defined as follows:
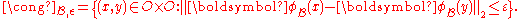
For notational convenience, this relation can be written instead of
instead of with the understanding that
with the understanding that  is inherent to the definition of the tolerance.
is inherent to the definition of the tolerance.
Tolerance classes are defined in terms of preclasses. Let denote that
denote that  is a perception-based preclass. Given
is a perception-based preclass. Given , then for all
, then for all 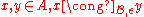 , i.e.,
, i.e.,
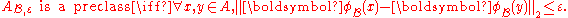
Let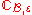 denote a tolerance class, which, by definition, is a maximal preclass. For
denote a tolerance class, which, by definition, is a maximal preclass. For  , we also use the notation
, we also use the notation to denote a tolerance class containing
to denote a tolerance class containing  . Note,
. Note,  covers
covers
 instead of partitioning
instead of partitioning
 because an object can belong to more than one class. In addition, each pair of objects
because an object can belong to more than one class. In addition, each pair of objects  in
in 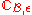 must satisfy the condition
must satisfy the condition 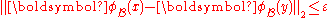 . Next, a covering
. Next, a covering
of defined by
defined by is the union of all tolerance classes in the covering.
is the union of all tolerance classes in the covering.
Notice that the tolerance relation is a generalization of the indiscernibility relation given in Defn. 5 (obtained by setting
is a generalization of the indiscernibility relation given in Defn. 5 (obtained by setting  ).
).
Definition 7: Weak Nearness Relation
Let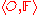 be a perceptual system and let
be a perceptual system and let  . A set
. A set  is weakly near to a set
is weakly near to a set  (denoted
(denoted 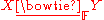 ) within the perceptual system
) within the perceptual system 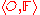 iff
iff
there are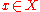 and
and  and there is
and there is such that
such that 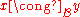 . Notice that the image given in the lead section is actually an example of sets that are weakly near each other (with
. Notice that the image given in the lead section is actually an example of sets that are weakly near each other (with  ).
).
Definition 8: Nearness Relation
Let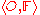 be perceptual system and let
be perceptual system and let  . A set
. A set  is near to a set
is near to a set  (denoted
(denoted  )within the perceptual system
)within the perceptual system 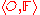 iff
iff
there are and
and 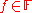 and there are
and there are 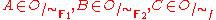 such that
such that  ,
,  and
and  .
.
The following simple example highlights the need for a tolerance relation as well as demonstrates the construction of tolerance classes from real data. Consider the 20 objects in the table below with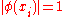 .
.
Letting gives the following tolerance classes:
gives the following tolerance classes:
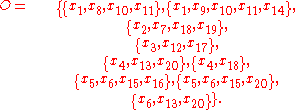
Observe that each object in a tolerance class satisfies the condition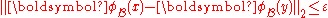 , and that almost all of the objects appear in more than one class. Moreover, there would be twenty classes if the indiscernibility relation was used since there are no two objects with matching descriptions. Finally, using these objects, the sets
, and that almost all of the objects appear in more than one class. Moreover, there would be twenty classes if the indiscernibility relation was used since there are no two objects with matching descriptions. Finally, using these objects, the sets
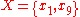 and
and 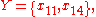
are weakly near each other.
Image Processing Example
The following example provides a more useful application of near set theory. Let a subimage be defined as a small subset of pixels
belonging to a digital image such that the pixels contained in the subimage form a square. Then, let the sets and
and  respectively represent the subimages obtained from two different images, and let
respectively represent the subimages obtained from two different images, and let 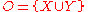 . Finally, let the description of an object be given by the Green component in the RGB color model
. Finally, let the description of an object be given by the Green component in the RGB color model
. The next step is to find all the tolerance classes using the tolerance relation. Using this information, tolerance classes can be formed containing objects that have similar (within some small ) values for the Green component in the RGB colour model. Furthermore, images that are near (similar) to each other should have tolerance classes divided among both images (instead of a tolerance classes contained solely in one of the images). For example, the figure accompanying this example shows a subset of the tolerance classes obtained from two leaf images. In this figure, each tolerance class is assigned a separate colour. As can be seen, the two leaves share similar tolerance classes. This example is a first step toward the application of near sets to the image correspondence problem. However, it also highlights a need to measure the degree of nearness of two sets.
) values for the Green component in the RGB colour model. Furthermore, images that are near (similar) to each other should have tolerance classes divided among both images (instead of a tolerance classes contained solely in one of the images). For example, the figure accompanying this example shows a subset of the tolerance classes obtained from two leaf images. In this figure, each tolerance class is assigned a separate colour. As can be seen, the two leaves share similar tolerance classes. This example is a first step toward the application of near sets to the image correspondence problem. However, it also highlights a need to measure the degree of nearness of two sets.
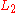 norm-based nearness measure is was developed. Specifically, it was based on the idea that sets can be considered near each other when they have "things" in common. In the context of near sets, the "things" can be quantified by granules of a perceptual system, i.e., the tolerance classes. The simplest example of nearness between sets sharing "things" in common is the case when two sets have similar elements. Defn. 7 can be used to define a Nearness Measure (NM) between two sets
norm-based nearness measure is was developed. Specifically, it was based on the idea that sets can be considered near each other when they have "things" in common. In the context of near sets, the "things" can be quantified by granules of a perceptual system, i.e., the tolerance classes. The simplest example of nearness between sets sharing "things" in common is the case when two sets have similar elements. Defn. 7 can be used to define a Nearness Measure (NM) between two sets  and
and  . Let
. Let  and let the notation
and let the notation
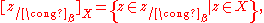
denote the portion of the tolerance class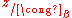 that belongs to
that belongs to  , and similarly, use the notation
, and similarly, use the notation
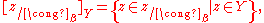
to denote the portion that belongs to . Further, let the sets
. Further, let the sets  and
and  be weakly near each other using Defn. 6. Also, let
be weakly near each other using Defn. 6. Also, let 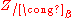 denote a covering of
denote a covering of  defined by
defined by  . Then, a
. Then, a 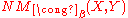 between
between  and
and  is given by
is given by
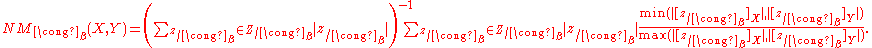
The idea behind the NM is that sets that are similar should have a similar number of objects in each tolerance class. Thus, for each tolerance class obtained from the covering of , the NM counts the number of objects that belong to
, the NM counts the number of objects that belong to  and
and  and takes the ratio (as a proper fraction) of their cardinalities. Furthermore, each ratio is weighted by the total size of the tolerance class (thus giving importance to the larger classes) and the final result is normalized by dividing by the sum of all the cardinalities. The range of the NM is in the interval [0,1], where a value of 1 is obtained if the sets are equivalent and a value of 0 is obtained if they have no elements in common.
and takes the ratio (as a proper fraction) of their cardinalities. Furthermore, each ratio is weighted by the total size of the tolerance class (thus giving importance to the larger classes) and the final result is normalized by dividing by the sum of all the cardinalities. The range of the NM is in the interval [0,1], where a value of 1 is obtained if the sets are equivalent and a value of 0 is obtained if they have no elements in common.
As an example of the degree of nearness between two sets, consider figure below in which each image consists of two sets of objects, and
and  . Each colour in the figures corresponds to an elementary set where all the objects in the class share the same description. The idea behind the NM is that the nearness of sets in a perceptual system is based on the cardinality of tolerance classes that they share. Thus, the sets in left side of the figure are closer (more near) to each other in terms of their descriptions than the sets in right side of the figure.
. Each colour in the figures corresponds to an elementary set where all the objects in the class share the same description. The idea behind the NM is that the nearness of sets in a perceptual system is based on the cardinality of tolerance classes that they share. Thus, the sets in left side of the figure are closer (more near) to each other in terms of their descriptions than the sets in right side of the figure.
Near set theory provides methods that can be used to extract resemblance information from objects contained in disjoint sets, i.e., it provides a formal basis for the observation, comparison, and classification of objects. The discovery of near sets begins with choosing the appropriate method to describe observed objects. This is accomplished by the selection of probe functions representing observable object features. A probe function is a mapping from an object to a real number representing a feature value. For example, when comparing fruit such as apples, the redness of an apple (observed object) can be described by a probe function representing colour, and the output of the probe function is a number representing the degree of redness (or whatever colour apple you prefer to eat). Probe functions provide a basis for describing and discerning affinities between objects as well as between groups of similar objects. Objects that have, in some degree, affinities are considered near each other. Similarly, groups of objects (i.e. sets) that have, in some degree, affinities are also considered near each other.
Near sets offer a framework for solving problems based on human perception
Perception
Perception is the process of attaining awareness or understanding of the environment by organizing and interpreting sensory information. All perception involves signals in the nervous system, which in turn result from physical stimulation of the sense organs...
that arise in areas such as image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
as well as engineering and science problems. In near set theory, perception is a combination of the view of perception in psychophysics
Psychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they effect. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, more completely, as "the analysis of perceptual...
with a view of perception found in Merleau-Ponty's
Maurice Merleau-Ponty
Maurice Merleau-Ponty was a French phenomenological philosopher, strongly influenced by Karl Marx, Edmund Husserl and Martin Heidegger in addition to being closely associated with Jean-Paul Sartre and Simone de Beauvoir...
work. In the context of psychophysics, perception of an object (i.e., in effect, knowledge about an object) depends on signal values gathered by our senses. In this view of perception, our senses are likened to probe functions by considering them as mappings of stimuli to sensations that are a source of values assimilated by the mind. A human sense modelled as a probe measures observable physical characteristics of objects in our environment. The sensed physical characteristics of an object are identified with object features. In Merleau-Ponty's view, an object is perceived to the extent that it can be described. In other words, object description goes hand-in-hand with object perception. It is the mind that identifies relationships between object descriptions to form perceptions of sensed objects. It is also the case that near set theory has been proven to be quite successful in finding solutions to perceptual problems such as measuring image correspondence and segmentation evaluation.

History
It has been observed that mathematical topics emerge and evolve through interactions among many researchers. This was the case with the discovery of near sets. Work on a perceptual basis for near sets began in 2002, motivated by digital image analysis. It was inspired by a study of the perception of nearness of familiar objects carried out by Z. Pawlak and J.F. Peters. In this context, nearness is interpreted to mean closely corresponding to or resembling an original. This collaboration was important in paving the way toward a description-based approach to exploring the nearness of sets.Excitement grew after 2002, when it became apparent that it was possible to introduce measures of nearness based on similarities between classes contained in coverings of disjoint sets (e.g., this is possible if we define coverings of sets representing digital images and then look for similarities between the images such as shades of green in one landscape that resemble one or more shades of green in another landscape). In this context the term similarity
Similarity
-Specific definitions:Different fields provide differing definitions of similarity:-In computer science:* string metric, aka string similarity* semantic similarity in computational linguistics-In other fields:...
means resemblance between two or more individual objects or sets of objects and almost equal patterns in compared items. Collaboration between J.F. Peters, A. Skowron, and J. Stepaniuk led to a formal basis for the nearness of objects considered in the context of proximity spaces
Proximity space
In topology, a proximity space is an axiomatization of notions of "nearness" that hold set-to-set, as opposed to the better known point-to-set notions that characterize topological spaces....
. Near sets and an approach to defining resemblance between sets was introduced by J.F. Peters in.
Near set theory and its applications grew out of a generalization of the approach to the classification of objects proposed by Z. Pawlak during his work on rough sets
Rough set
In computer science, a rough set, first described by a Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set...
in the early 1980s, and E. Orłowska's work on approximation spaces. Briefly, a rough set can be described as follows. Consider a non-empty finite set of objects labelled
 . The set
. The set  can be partitioned
can be partitionedPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into cells (referred to as classes in near set theory) by grouping together objects that have similar descriptions (using one or more probe functions). A set
 is considered rough when it cannot be formed completely by the union of classes from the partition of
is considered rough when it cannot be formed completely by the union of classes from the partition of  . The set
. The set  is considered rough inasmuch as
is considered rough inasmuch as  cannot be fully described by probe functions selected to describe the individual objects of
cannot be fully described by probe functions selected to describe the individual objects of  .
.Near sets are considered a generalization of rough sets, since it has been shown that every rough set is a near set but not every near set is a rough set. Near sets grew out of the idea that two or more rough sets can share objects with matching descriptions if they both contain objects belonging to the same class from the partition of
 . When this occurs, the sets are considered near each other with respect to the classes contained in the partition.
. When this occurs, the sets are considered near each other with respect to the classes contained in the partition.Definitions
Definition 1: ObjectAn object is anything that has its origin in the physical world.
An identifying characteristic of an object is that it must have some quantifiable features. The term feature is used in S. Watanabe's sense of the word, i.e., a feature corresponds to an observable property of physical objects. Each feature has a 1-to-many relationship to real-valued functions called probe functions representing the feature. For each feature (such as colour) one or more probe functions can be introduced to represent the feature (such as grayscale
Grayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
, or RGB
RGB color model
The RGB color model is an additive color model in which red, green, and blue light is added together in various ways to reproduce a broad array of colors...
values). Objects and sets of probe functions form the basis of near set theory and are sometimes referred to as perceptual objects due to the focus on assigning values to perceived object features. A non-empty, finite set of objects is denoted by
 .
.Definition 2: Probe Function
A probe function is a real-valued function,
 , representing a feature of an object.
, representing a feature of an object.Examples of probe functions are the colour, size, texture, edge-orientation, or weight of an object. Probe functions are used to describe an object to determine the characteristics and perceptual similarity of objects. Perceptual information is always presented with respect to probe functions just as our senses define our perception of the world. For example, our ability to view light in the visible spectrumrather than infra red or microwaves spectra defines our perception of the world just as the selection of probe functions constrains the amount of perceptual information available for feature extraction from a set of objects. The set of all probe functions is denoted by
 , and a set of specific probe functions for a given application is denoted by
, and a set of specific probe functions for a given application is denoted by 
Definition 3: Perceptual System
A perceptual system
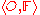 consists of a non-empty set
consists of a non-empty set  together with a set
together with a set  of real-valued functions.
of real-valued functions.The notion of a perceptual system admits a wide variety of different interpretations that result from the selection of sample objects contained in a particular sample space
 . A recent example of a perceptual system is given by D. Hall. Two other examples of perceptual systems are: a set of microscope images together with a set of image processing probe functions, or a set of results from a web query together with some measures (probe functions) indicating, e.g., relevancy of the results.
. A recent example of a perceptual system is given by D. Hall. Two other examples of perceptual systems are: a set of microscope images together with a set of image processing probe functions, or a set of results from a web query together with some measures (probe functions) indicating, e.g., relevancy of the results.Definition 4: Object Description
Consider a perceptual system
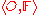 . The description of an object
. The description of an object 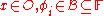 is given by the vector
is given by the vector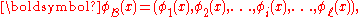
where
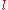 is the length of the vector
is the length of the vector  , and each
, and each 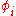 is a probe function belonging to the set
is a probe function belonging to the set 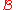 .
.Definition 5: Perceptual Indiscernibility Relation
Let
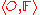 be a perceptual system. For every
be a perceptual system. For every  the perceptual indiscernibility relation
the perceptual indiscernibility relation 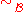 is defined as follows:
is defined as follows: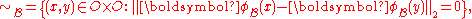
where
 represents the
represents the 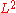 norm
normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. This is a refinement of the original indiscernibility relation given by Pawlak in 1981. Using the perceptual indiscernibility relation, objects with matching descriptions can be grouped to form classes called elementary sets (also called an equivalence class) defined by
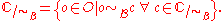
Similarly, a quotient set is the set of all elementary sets defined as
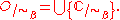
Definition 6: Perceptual Tolerance Relation
When dealing with perceptual objects (especially, components in images), it is sometimes necessary to relax the equivalence condition of Defn. 5 to facilitate observation of associations in a perceptual system. This variation is called a perceptual tolerance relation. Let
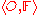 be a perceptual system and let
be a perceptual system and let 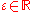 . For every
. For every the tolerance relation
the tolerance relation  is defined as follows:
is defined as follows: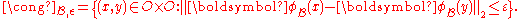
For notational convenience, this relation can be written
 instead of
instead of with the understanding that
with the understanding that  is inherent to the definition of the tolerance.
is inherent to the definition of the tolerance.Tolerance classes are defined in terms of preclasses. Let
 denote that
denote that  is a perception-based preclass. Given
is a perception-based preclass. Given , then for all
, then for all 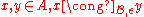 , i.e.,
, i.e.,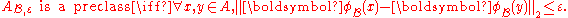
Let
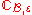 denote a tolerance class, which, by definition, is a maximal preclass. For
denote a tolerance class, which, by definition, is a maximal preclass. For  , we also use the notation
, we also use the notation to denote a tolerance class containing
to denote a tolerance class containing  . Note,
. Note,  covers
coversCover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
 instead of partitioning
instead of partitioningPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
 because an object can belong to more than one class. In addition, each pair of objects
because an object can belong to more than one class. In addition, each pair of objects  in
in 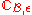 must satisfy the condition
must satisfy the condition 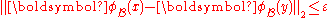 . Next, a covering
. Next, a coveringCover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
of
 defined by
defined by is the union of all tolerance classes in the covering.
is the union of all tolerance classes in the covering.Notice that the tolerance relation
 is a generalization of the indiscernibility relation given in Defn. 5 (obtained by setting
is a generalization of the indiscernibility relation given in Defn. 5 (obtained by setting  ).
).Definition 7: Weak Nearness Relation
Let
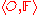 be a perceptual system and let
be a perceptual system and let  . A set
. A set  is weakly near to a set
is weakly near to a set  (denoted
(denoted 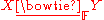 ) within the perceptual system
) within the perceptual system 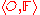 iff
iffIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there are
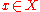 and
and  and there is
and there is such that
such that 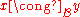 . Notice that the image given in the lead section is actually an example of sets that are weakly near each other (with
. Notice that the image given in the lead section is actually an example of sets that are weakly near each other (with  ).
).Definition 8: Nearness Relation
Let
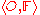 be perceptual system and let
be perceptual system and let  . A set
. A set  is near to a set
is near to a set  (denoted
(denoted  )within the perceptual system
)within the perceptual system 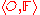 iff
iffIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there are
 and
and 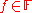 and there are
and there are 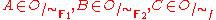 such that
such that  ,
,  and
and  .
.Examples
Simple ExampleThe following simple example highlights the need for a tolerance relation as well as demonstrates the construction of tolerance classes from real data. Consider the 20 objects in the table below with
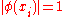 .
. |  |  |  | 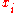 | 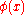 | 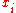 | 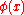 |
|---|---|---|---|---|---|---|---|
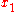 |
.4518 | 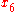 |
.6943 | 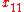 |
.4002 | 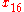 |
.6079 |
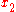 |
.9166 | 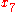 |
.9246 | 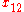 |
.1910 | 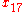 |
.1869 |
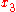 |
.1398 |  |
.3537 | 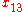 |
.7476 | 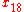 |
.8489 |
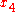 |
.7972 | 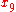 |
.4722 | 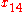 |
.4990 | 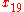 |
.9170 |
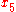 |
.6281 | 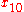 |
.4523 | 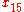 |
.6289 | 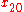 |
.7143 |
Letting
 gives the following tolerance classes:
gives the following tolerance classes: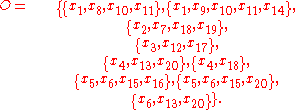
Observe that each object in a tolerance class satisfies the condition
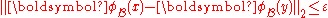 , and that almost all of the objects appear in more than one class. Moreover, there would be twenty classes if the indiscernibility relation was used since there are no two objects with matching descriptions. Finally, using these objects, the sets
, and that almost all of the objects appear in more than one class. Moreover, there would be twenty classes if the indiscernibility relation was used since there are no two objects with matching descriptions. Finally, using these objects, the sets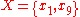 and
and 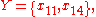
are weakly near each other.
Image Processing Example
The following example provides a more useful application of near set theory. Let a subimage be defined as a small subset of pixels
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
belonging to a digital image such that the pixels contained in the subimage form a square. Then, let the sets
 and
and  respectively represent the subimages obtained from two different images, and let
respectively represent the subimages obtained from two different images, and let 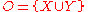 . Finally, let the description of an object be given by the Green component in the RGB color model
. Finally, let the description of an object be given by the Green component in the RGB color modelRGB color model
The RGB color model is an additive color model in which red, green, and blue light is added together in various ways to reproduce a broad array of colors...
. The next step is to find all the tolerance classes using the tolerance relation. Using this information, tolerance classes can be formed containing objects that have similar (within some small
 ) values for the Green component in the RGB colour model. Furthermore, images that are near (similar) to each other should have tolerance classes divided among both images (instead of a tolerance classes contained solely in one of the images). For example, the figure accompanying this example shows a subset of the tolerance classes obtained from two leaf images. In this figure, each tolerance class is assigned a separate colour. As can be seen, the two leaves share similar tolerance classes. This example is a first step toward the application of near sets to the image correspondence problem. However, it also highlights a need to measure the degree of nearness of two sets.
) values for the Green component in the RGB colour model. Furthermore, images that are near (similar) to each other should have tolerance classes divided among both images (instead of a tolerance classes contained solely in one of the images). For example, the figure accompanying this example shows a subset of the tolerance classes obtained from two leaf images. In this figure, each tolerance class is assigned a separate colour. As can be seen, the two leaves share similar tolerance classes. This example is a first step toward the application of near sets to the image correspondence problem. However, it also highlights a need to measure the degree of nearness of two sets.Nearness measure
For some applications it is not sufficient to simply state that two sets are near each other. The practical application of near set theory sometimes requires a method for quantifying the nearness of sets. As a result, a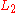 norm-based nearness measure is was developed. Specifically, it was based on the idea that sets can be considered near each other when they have "things" in common. In the context of near sets, the "things" can be quantified by granules of a perceptual system, i.e., the tolerance classes. The simplest example of nearness between sets sharing "things" in common is the case when two sets have similar elements. Defn. 7 can be used to define a Nearness Measure (NM) between two sets
norm-based nearness measure is was developed. Specifically, it was based on the idea that sets can be considered near each other when they have "things" in common. In the context of near sets, the "things" can be quantified by granules of a perceptual system, i.e., the tolerance classes. The simplest example of nearness between sets sharing "things" in common is the case when two sets have similar elements. Defn. 7 can be used to define a Nearness Measure (NM) between two sets  and
and  . Let
. Let  and let the notation
and let the notation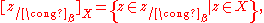
denote the portion of the tolerance class
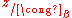 that belongs to
that belongs to  , and similarly, use the notation
, and similarly, use the notation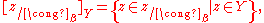
to denote the portion that belongs to
 . Further, let the sets
. Further, let the sets  and
and  be weakly near each other using Defn. 6. Also, let
be weakly near each other using Defn. 6. Also, let 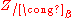 denote a covering of
denote a covering of  defined by
defined by  . Then, a
. Then, a 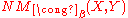 between
between  and
and  is given by
is given by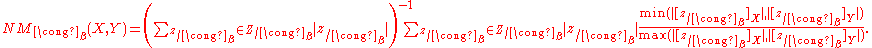
The idea behind the NM is that sets that are similar should have a similar number of objects in each tolerance class. Thus, for each tolerance class obtained from the covering of
 , the NM counts the number of objects that belong to
, the NM counts the number of objects that belong to  and
and  and takes the ratio (as a proper fraction) of their cardinalities. Furthermore, each ratio is weighted by the total size of the tolerance class (thus giving importance to the larger classes) and the final result is normalized by dividing by the sum of all the cardinalities. The range of the NM is in the interval [0,1], where a value of 1 is obtained if the sets are equivalent and a value of 0 is obtained if they have no elements in common.
and takes the ratio (as a proper fraction) of their cardinalities. Furthermore, each ratio is weighted by the total size of the tolerance class (thus giving importance to the larger classes) and the final result is normalized by dividing by the sum of all the cardinalities. The range of the NM is in the interval [0,1], where a value of 1 is obtained if the sets are equivalent and a value of 0 is obtained if they have no elements in common.As an example of the degree of nearness between two sets, consider figure below in which each image consists of two sets of objects,
 and
and  . Each colour in the figures corresponds to an elementary set where all the objects in the class share the same description. The idea behind the NM is that the nearness of sets in a perceptual system is based on the cardinality of tolerance classes that they share. Thus, the sets in left side of the figure are closer (more near) to each other in terms of their descriptions than the sets in right side of the figure.
. Each colour in the figures corresponds to an elementary set where all the objects in the class share the same description. The idea behind the NM is that the nearness of sets in a perceptual system is based on the cardinality of tolerance classes that they share. Thus, the sets in left side of the figure are closer (more near) to each other in terms of their descriptions than the sets in right side of the figure.Near set evaluation and recognition (NEAR) system
The Near set Evaluation and Recognition (NEAR) system, is a system developed to demonstrate practical applications of near set theory to the problems of image segmentation evaluation and image correspondence. It was motivated by a need for a freely available software tool that can provide results for research and to generate interest in near set theory. The system implements a Multiple Document Interface (MDI) where each separate processing task is performed in its own child frame. The objects (in the near set sense) in this system are subimages of the images being processed and the probe functions (features) are image processing functions defined on the subimages. The system was written in C++ and was designed to facilitate the addition of new processing tasks and probe functions. Currently, the system performs five major tasks, namely, displaying equivalence and tolerance classes for an image, performing segmentation evaluation, measuring the nearness of two images, and displaying the output of processing an image using an individual probe functions.Further reading
- Henry, C., Peters, J.F. Near set evaluation and recognition (NEAR) system. Tech. rep., Computational Intelligence Laboratory, University of Manitoba, UM CI Laboratory Technical Report No. TR-2009-015, 2009.
- Peters, J.F., Wasilewski, P. Foundations of near sets. Information Sciences 179 (18), 2009, 3091-3109.
- Pavel, M. Fundamentals of Pattern Recognition, 2nd ed. Pure and Applied Mathematics, vol. 174, Marcel Dekker, Inc., 1993.
External links
- Pal, S.K., Peters, J.F., Eds. Rough Fuzzy Image Analysis. Foundations and Methodologies. Routledge, 2010, ISBN 978-1-4398-0329-5. To appear in September 2010. Many chapters present the theory and application of near sets in image analysis, including several system implementations.
- Hassanien, E., Abraham, A., Peters, J.F., Schaefer, G., Henry, C. Rough sets and near sets in medical imaging: A review. IEEE Trans. on Information Technology in Biomedicine 13 (5), 2009, doi: 10.1109/TITB.2009.2017017.

