On Spirals
Encyclopedia
On Spirals is a treatise by Archimedes
in 225 BC
. Although Archimedes did not discover the Archimedean spiral
, he employed it in this book to square the circle and trisect an angle.
as a loss to mathematics. He then goes on to summarize the results of On the Sphere and Cylinder
and On Conoids and Spheroids. He continues to state his results of On Spirals.
 The Archimedean spiral was first studied by Conon
The Archimedean spiral was first studied by Conon
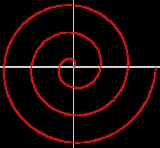
and was later studied by Archimedes in On Spirals. Archimedes was able to find various tangents to the spiral. He defines the spiral as:
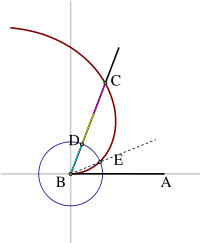 The construction as to how Archimedes trisected the angle is as follows:
The construction as to how Archimedes trisected the angle is as follows:
 To square the circle, Archimedes gave the following construction:
To square the circle, Archimedes gave the following construction:
Archimedes had already proved as the first proposition of Measurement of a Circle
that the area of a circle is equal to a right-angled triangle having the legs' lengths equal to the radius of the circle and the circumference of the circle. So the area of the circle with radius OP is equal to the area of the triangle OPT.
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
in 225 BC
225 BC
Year 225 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Papus and Regulus...
. Although Archimedes did not discover the Archimedean spiral
Archimedean spiral
The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
, he employed it in this book to square the circle and trisect an angle.
Preface
Archimedes begins On Spirals with a message to Dositheus of Pelusium mentioning the death of CononConon of Samos
Conon of Samos was a Greek astronomer and mathematician. He is primarily remembered for naming the constellation Coma Berenices.-Life and work:...
as a loss to mathematics. He then goes on to summarize the results of On the Sphere and Cylinder
On the Sphere and Cylinder
On the Sphere and Cylinder is a work that was published by Archimedes in two volumes c. 225 BC. It most notably details how to find the surface area of a sphere and the volume of the contained ball and the analogous values for a cylinder, and was the first to do so.-Contents:The principal formulae...
and On Conoids and Spheroids. He continues to state his results of On Spirals.
Archimedean spiral

Conon of Samos
Conon of Samos was a Greek astronomer and mathematician. He is primarily remembered for naming the constellation Coma Berenices.-Life and work:...
and was later studied by Archimedes in On Spirals. Archimedes was able to find various tangents to the spiral. He defines the spiral as:
Trisecting an angle

Suppose the angle ABC is to be trisected. Trisect the segment BC and find BD to be one third of BC. Draw a circle with center B and radius BD. Suppose the circle with center B intersects the spiral at point E. Angle ABE is one third angle ABC.
Squaring the circle

Let P be the point on the spiral when it has completed one turn. Let the tangent at P cut the line perpendicular to OP at T. OT is the length of the circumference of the circle with radius OP.
Archimedes had already proved as the first proposition of Measurement of a Circle
Measurement of a Circle
Measurement of a Circle is a treatise that consists of three propositions by Archimedes. The treatise is only a fraction of what was a longer work.-Proposition one:Proposition one states:...
that the area of a circle is equal to a right-angled triangle having the legs' lengths equal to the radius of the circle and the circumference of the circle. So the area of the circle with radius OP is equal to the area of the triangle OPT.

