
Peter–Weyl theorem
Encyclopedia
In mathematics
, the Peter–Weyl theorem is a basic result in the theory of harmonic analysis
, applying to topological group
s that are compact
, but are not necessarily abelian. It was initially proved by Hermann Weyl
, with his student Fritz Peter
, in the setting of a compact topological group
G . The theorem is a collection of results generalizing the significant facts about the decomposition of the regular representation
of any finite group, as discovered by F. G. Frobenius and Issai Schur
.
The theorem has three parts. The first part states that the matrix coefficients of irreducible representations of G are dense in the space C(G) of continuous complex-valued functions on G, and thus also in the space L2(G) of square-integrable functions. The second part asserts the complete reducibility of unitary representations of G. The third part then asserts that the regular representation of G on L2(G) decomposes as the direct sum of all irreducible unitary representations. Moreover, the matrix coefficients of the irreducible unitary representations form an orthonormal basis of L2(G).
of the group G is a complex-valued function on G given as the composition
on G given as the composition
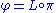
where π : G → GL(V) is a finite-dimensional (continuous
) group representation
of G, and L is a linear functional
on the vector space of endomorphism
s of V (e.g. trace), which contains GL(V) as an open subset. Matrix coefficients are continuous, since representations are by definition continuous, and linear functionals on finite-dimensional spaces are also continuous.
The first part of the Peter–Weyl theorem asserts :
This first result resembles the Stone-Weierstrass theorem
in that it indicates the density of a set of functions in the space of all continuous functions, subject only to an algebraic characterization. In fact, if G is a matrix group
, then the result follows easily from the Stone-Weierstrass theorem . Conversely, it is a consequence of the subsequent conclusions of the theorem that any compact Lie group
is isomorphic to a matrix group .
A corollary of this result is that the matrix coefficients of G are dense in L2(G).
of G into finite-dimensional representations. Now, intuitively groups were conceived as rotations on geometric objects, so it is only natural to study representations which essentially arise from continuous actions
on Hilbert spaces. (For those who were first introduced to dual groups consisting of characters which are the continuous homomorphisms into the circle group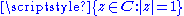 , this approach is similar except that the circle group is (ultimately) generalised to the group of unitary operators on a given Hilbert space.)
, this approach is similar except that the circle group is (ultimately) generalised to the group of unitary operators on a given Hilbert space.)
Let G be a topological group and H a complex Hilbert space.
A continuous action , gives rise to a map
, gives rise to a map 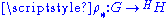 defined in the obvious way:
defined in the obvious way:  . This map is clearly an homomorphism from G into GL(H), the homeomorphic automorphisms of H. And given such a map, we can uniquely recover the action in the obvious way.
. This map is clearly an homomorphism from G into GL(H), the homeomorphic automorphisms of H. And given such a map, we can uniquely recover the action in the obvious way.
Thus we define the representations of G on an Hilbert space H to be those group homomorphisms, ρ, which arise from continuous actions of G on H. We say that a representation ρ is unitary if ρ(g) is a unitary operator
for all g ∈ G; i.e., for all v, w ∈ H. (I.e. it is unitary if
for all v, w ∈ H. (I.e. it is unitary if 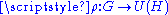 . Notice how this generalises the special case of the one-dimensional Hilbert space, where U(C) is just the circle group.)
. Notice how this generalises the special case of the one-dimensional Hilbert space, where U(C) is just the circle group.)
Given these definitions, we can state the second part of the Peter–Weyl theorem :
s, L2(G)
; this makes sense because Haar measure
exists on G. Calling this Hilbert space H, the group G has a unitary representation
ρ on H by acting
on the left, via

The final statement of the Peter–Weyl theorem gives an explicit orthonormal basis
of L2(G). Roughly it asserts that the matrix coefficients for G, suitably renormalized, are an orthonormal basis
of L2(G). In particular, L2(G) decomposes into an orthogonal direct sum of all the irreducible unitary representations, in which the multiplicity of each irreducible representation is equal to its degree (that is, the dimension of the underlying space of the representation). Thus,
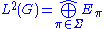
where Σ denotes the set of (isomorphism classes of) irreducible unitary representations of G, and the summation denotes the closure
of the direct sum of the total spaces Eπ of the representations π.
More precisely, suppose that a representative π is chosen for each isomorphism class of irreducible unitary representation, and denote the collection of all such π by Σ. Let be the matrix coefficients of π in an orthonormal basis, in other words
be the matrix coefficients of π in an orthonormal basis, in other words

for each g ∈ G. Finally, let d(π) be the degree of the representation π. The theorem now asserts that the set of functions
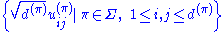
is an orthonormal basis of L2(G).
. For any finite-dimensional G-invariant subspace V in L2(G), where G acts
on the left, we consider the image of G in GL(V). It is closed, since G is compact, and a subgroup of the Lie group
GL(V). It follows by a theorem
of Élie Cartan
that the image of G is a Lie group also.
If we now take the limit (in the sense of category theory
) over all such spaces V, we get a result about G - because G acts faithfully on L2(G). We can say that G is an inverse limit of Lie groups. It may of course not itself be a Lie group: it may for example be a profinite group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Peter–Weyl theorem is a basic result in the theory of harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, applying to topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s that are compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
, but are not necessarily abelian. It was initially proved by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, with his student Fritz Peter
Fritz Peter
Fritz Peter was a German mathematician who helped prove the Peter–Weyl theorem. He was a student of Hermann Weyl, and later became headmaster of a secondary school ....
, in the setting of a compact topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
G . The theorem is a collection of results generalizing the significant facts about the decomposition of the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
of any finite group, as discovered by F. G. Frobenius and Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
.
The theorem has three parts. The first part states that the matrix coefficients of irreducible representations of G are dense in the space C(G) of continuous complex-valued functions on G, and thus also in the space L2(G) of square-integrable functions. The second part asserts the complete reducibility of unitary representations of G. The third part then asserts that the regular representation of G on L2(G) decomposes as the direct sum of all irreducible unitary representations. Moreover, the matrix coefficients of the irreducible unitary representations form an orthonormal basis of L2(G).
Matrix coefficients
A matrix coefficientMatrix coefficient
In mathematics, a matrix coefficient is a function on agroup of a special form, which depends on a linear representation of the group and additional data...
of the group G is a complex-valued function
 on G given as the composition
on G given as the composition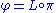
where π : G → GL(V) is a finite-dimensional (continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
) group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G, and L is a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on the vector space of endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of V (e.g. trace), which contains GL(V) as an open subset. Matrix coefficients are continuous, since representations are by definition continuous, and linear functionals on finite-dimensional spaces are also continuous.
The first part of the Peter–Weyl theorem asserts :
- The set of matrix coefficients of G is denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the space of continuous complex functionsContinuous functions on a compact Hausdorff spaceIn mathematical analysis, and especially functional analysis, a fundamental role is played by the space of continuous functions on a compact Hausdorff space with values in the real or complex numbers. This space, denoted by C, is a vector space with respect to the pointwise addition of functions...
C(G) on G, equipped with the uniform norm.
This first result resembles the Stone-Weierstrass theorem
Stone-Weierstrass theorem
In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
in that it indicates the density of a set of functions in the space of all continuous functions, subject only to an algebraic characterization. In fact, if G is a matrix group
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
, then the result follows easily from the Stone-Weierstrass theorem . Conversely, it is a consequence of the subsequent conclusions of the theorem that any compact Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is isomorphic to a matrix group .
A corollary of this result is that the matrix coefficients of G are dense in L2(G).
Decomposition of a unitary representation
The second part of the theorem gives the existence of a decomposition of a unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of G into finite-dimensional representations. Now, intuitively groups were conceived as rotations on geometric objects, so it is only natural to study representations which essentially arise from continuous actions
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on Hilbert spaces. (For those who were first introduced to dual groups consisting of characters which are the continuous homomorphisms into the circle group
 , this approach is similar except that the circle group is (ultimately) generalised to the group of unitary operators on a given Hilbert space.)
, this approach is similar except that the circle group is (ultimately) generalised to the group of unitary operators on a given Hilbert space.)Let G be a topological group and H a complex Hilbert space.
A continuous action
 , gives rise to a map
, gives rise to a map 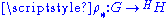 defined in the obvious way:
defined in the obvious way:  . This map is clearly an homomorphism from G into GL(H), the homeomorphic automorphisms of H. And given such a map, we can uniquely recover the action in the obvious way.
. This map is clearly an homomorphism from G into GL(H), the homeomorphic automorphisms of H. And given such a map, we can uniquely recover the action in the obvious way.Thus we define the representations of G on an Hilbert space H to be those group homomorphisms, ρ, which arise from continuous actions of G on H. We say that a representation ρ is unitary if ρ(g) is a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
for all g ∈ G; i.e.,
 for all v, w ∈ H. (I.e. it is unitary if
for all v, w ∈ H. (I.e. it is unitary if 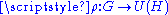 . Notice how this generalises the special case of the one-dimensional Hilbert space, where U(C) is just the circle group.)
. Notice how this generalises the special case of the one-dimensional Hilbert space, where U(C) is just the circle group.)Given these definitions, we can state the second part of the Peter–Weyl theorem :
- Let ρ be a unitary representation of a compact group G on a complex Hilbert space H. Then H splits into an orthogonal direct sum of irreducible finite-dimensional unitary representations of G.
Decomposition of square-integrable functions
To state the third and final part of the theorem, there is a natural Hilbert space over G consisting of square-integrable functionSquare-integrable function
In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
s, L2(G)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
; this makes sense because Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
exists on G. Calling this Hilbert space H, the group G has a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
ρ on H by acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the left, via

The final statement of the Peter–Weyl theorem gives an explicit orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of L2(G). Roughly it asserts that the matrix coefficients for G, suitably renormalized, are an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of L2(G). In particular, L2(G) decomposes into an orthogonal direct sum of all the irreducible unitary representations, in which the multiplicity of each irreducible representation is equal to its degree (that is, the dimension of the underlying space of the representation). Thus,
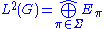
where Σ denotes the set of (isomorphism classes of) irreducible unitary representations of G, and the summation denotes the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the direct sum of the total spaces Eπ of the representations π.
More precisely, suppose that a representative π is chosen for each isomorphism class of irreducible unitary representation, and denote the collection of all such π by Σ. Let
 be the matrix coefficients of π in an orthonormal basis, in other words
be the matrix coefficients of π in an orthonormal basis, in other words
for each g ∈ G. Finally, let d(π) be the degree of the representation π. The theorem now asserts that the set of functions
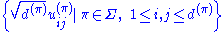
is an orthonormal basis of L2(G).
Structure of compact topological groups
From the theorem, one can deduce a significant general structure theorem. Let G be a compact topological group, which we assume HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. For any finite-dimensional G-invariant subspace V in L2(G), where G acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the left, we consider the image of G in GL(V). It is closed, since G is compact, and a subgroup of the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
GL(V). It follows by a theorem
Cartan's theorem
In mathematics, three results in Lie group theory are called Cartan's theorem, named after Élie Cartan:See also Cartan's theorems A and B, results of Henri Cartan, and Cartan's lemma for various other results attributed to Élie and Henri Cartan....
of Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
that the image of G is a Lie group also.
If we now take the limit (in the sense of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
) over all such spaces V, we get a result about G - because G acts faithfully on L2(G). We can say that G is an inverse limit of Lie groups. It may of course not itself be a Lie group: it may for example be a profinite group.

