Reciprocal Gamma function
Encyclopedia
In mathematics
, the reciprocal Gamma function is the function
where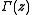
denotes the Gamma function
. Since the Gamma function is meromorphic
and nonzero everywhere in the complex plane
, its reciprocal is an entire function
. The reciprocal is sometimes used as a starting point for numerical computation
of the Gamma function, and a few software libraries provide it separately from the regular Gamma function.
Karl Weierstrass
called the reciprocal Gamma function the "factorielle" and used it in his development of the Weierstrass factorization theorem
.
expansion around 0 gives
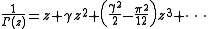
where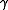
is the Euler-Mascheroni constant
. For k > 2, the coefficient ak for the zk term can be computed recursively as
where ζ(s) is the Riemann zeta function. For small values, this gives the following values:
is
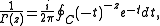
where C is a path encircling 0 in the positive direction, beginning at and returning to positive infinity with respect for the branch cut along the positive real axis. According to Schmelzer & Trefethen, numerical evaluation of Hankel's integral is the basis of some of the best methods for computing the Gamma function.
which is known as the Fransén–Robinson constant.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the reciprocal Gamma function is the function
where
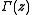denotes the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. Since the Gamma function is meromorphic
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
and nonzero everywhere in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, its reciprocal is an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
. The reciprocal is sometimes used as a starting point for numerical computation
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
of the Gamma function, and a few software libraries provide it separately from the regular Gamma function.
Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
called the reciprocal Gamma function the "factorielle" and used it in his development of the Weierstrass factorization theorem
Weierstrass factorization theorem
In mathematics, the Weierstrass factorization theorem in complex analysis, named after Karl Weierstrass, asserts that entire functions can be represented by a product involving their zeroes...
.
Taylor series
Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion around 0 gives
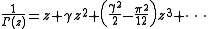
where
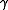is the Euler-Mascheroni constantEuler-Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
. For k > 2, the coefficient ak for the zk term can be computed recursively as
where ζ(s) is the Riemann zeta function. For small values, this gives the following values:
| k |  |
|---|---|
| 1 | 1.0000000000000000000000000000000000000000 |
| 2 | 0.5772156649015328606065120900824024310422 |
| 3 | -0.6558780715202538810770195151453904812798 |
| 4 | -0.0420026350340952355290039348754298187114 |
| 5 | 0.1665386113822914895017007951021052357178 |
| 6 | -0.0421977345555443367482083012891873913017 |
| 7 | -0.0096219715278769735621149216723481989754 |
| 8 | 0.0072189432466630995423950103404465727099 |
| 9 | -0.0011651675918590651121139710840183886668 |
| 10 | -0.0002152416741149509728157299630536478065 |
| 11 | 0.0001280502823881161861531986263281643234 |
| 12 | -0.0000201348547807882386556893914210218184 |
| 13 | -0.0000012504934821426706573453594738330922 |
| 14 | 0.0000011330272319816958823741296203307449 |
| 15 | -0.0000002056338416977607103450154130020573 |
| 16 | 0.0000000061160951044814158178624986828553 |
| 17 | 0.0000000050020076444692229300556650480600 |
| 18 | -0.0000000011812745704870201445881265654365 |
| 19 | 0.0000000001043426711691100510491540332312 |
| 20 | 0.0000000000077822634399050712540499373114 |
| 21 | -0.0000000000036968056186422057081878158781 |
| 22 | 0.0000000000005100370287454475979015481323 |
| 23 | -0.0000000000000205832605356650678322242954 |
| 24 | -0.0000000000000053481225394230179823700173 |
| 25 | 0.0000000000000012267786282382607901588938 |
| 26 | -0.0000000000000001181259301697458769513765 |
| 27 | 0.0000000000000000011866922547516003325798 |
| 28 | 0.0000000000000000014123806553180317815558 |
| 29 | -0.0000000000000000002298745684435370206592 |
| 30 | 0.0000000000000000000171440632192733743338 |
Contour integral representation
An integral representation due to Hermann HankelHermann Hankel
Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
is
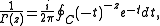
where C is a path encircling 0 in the positive direction, beginning at and returning to positive infinity with respect for the branch cut along the positive real axis. According to Schmelzer & Trefethen, numerical evaluation of Hankel's integral is the basis of some of the best methods for computing the Gamma function.
Integral along the real axis
Integration of the reciprocal Gamma function along the positive real axis gives the valuewhich is known as the Fransén–Robinson constant.