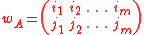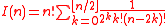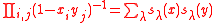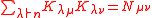Robinson–Schensted–Knuth correspondence
Encyclopedia
In mathematics
, the Robinson–Schensted–Knuth correspondence, also referred to as the RSK correspondence or RSK algorithm, is a combinatorial bijection
between matrices with non-negative integer entries and pairs of semistandard Young tableaux of equal shape, whose size equals the sum of the entries of . More precisely the weight of is given by the column sums of , and the weight of by its row sums.
It is a generalization of the Robinson–Schensted correspondence, in the sense that taking to be a permutation matrix
, the pair will be the pair of standard tableaux associated to the permutation under the Robinson–Schensted correspondence.
The Robinson–Schensted–Knuth correspondence extends many of the remarkable properties of the Robinson–Schensted correspondence, notably its symmetry: transposition of the matrix results in interchange of the tableaux .
s and pairs of standard Young tableau
x, both having the same shape. This bijection can be constructed using an algorithm called Schensted insertion, starting with an empty tableau and successively inserting the values σ1,…,σn of the permutation σ at the numbers 1,2,…n; these for the second line when σ is given in two-line form
.
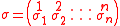The resulting standard tableau is the first of the pair corresponding to σ; the other standard tableau records the successive shapes of the intermediate tableaux during the construction of .
The Schensted insertion can in fact handle more general sequences of numbers than those arising from permutations (notably repeated entries are allowed); in that case it will produce a semistandard tableau rather than a standard tableau, but will still be a standard tableau. The definition of the RSK correspondence reestablishes symmetry between the tableaux by producing a semistandard tableau for as well.
in which for any pair that indexes an entry of , there are columns equal to
, and all columns are in lexicographic order, which means that
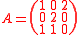
is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Robinson–Schensted–Knuth correspondence, also referred to as the RSK correspondence or RSK algorithm, is a combinatorial bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between matrices with non-negative integer entries and pairs of semistandard Young tableaux of equal shape, whose size equals the sum of the entries of . More precisely the weight of is given by the column sums of , and the weight of by its row sums.
It is a generalization of the Robinson–Schensted correspondence, in the sense that taking to be a permutation matrix
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
, the pair will be the pair of standard tableaux associated to the permutation under the Robinson–Schensted correspondence.
The Robinson–Schensted–Knuth correspondence extends many of the remarkable properties of the Robinson–Schensted correspondence, notably its symmetry: transposition of the matrix results in interchange of the tableaux .
Introduction
The Robinson–Schensted correspondence is a bijective mapping between permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s and pairs of standard Young tableau
Young tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x, both having the same shape. This bijection can be constructed using an algorithm called Schensted insertion, starting with an empty tableau and successively inserting the values σ1,…,σn of the permutation σ at the numbers 1,2,…n; these for the second line when σ is given in two-line form
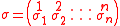.The resulting standard tableau is the first of the pair corresponding to σ; the other standard tableau records the successive shapes of the intermediate tableaux during the construction of .
The Schensted insertion can in fact handle more general sequences of numbers than those arising from permutations (notably repeated entries are allowed); in that case it will produce a semistandard tableau rather than a standard tableau, but will still be a standard tableau. The definition of the RSK correspondence reestablishes symmetry between the tableaux by producing a semistandard tableau for as well.
Two-line arrays
The two-line array (or generalized permutation) corresponding to a matrix is defined as
in which for any pair that indexes an entry of , there are columns equal to
, and all columns are in lexicographic order, which means that
-
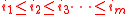, and - if
and 
then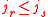 
.
Example
The two-line array corresponding to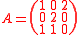is
-
Definition of the correspondence
By applying the Schensted insertion algorithm to the bottom line of this two-line array, one obtains a pair consisting of a semistandard tableau and a standard tableau , where the latter can be turned into a semistandard tableau by replacing each entry of by the -th entry of the top line of . One thus obtains a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from matrices to ordered pairs, of semistandard Young tableaux of the same shape, in which the set of entries of is that of the second line of , and the set of entries of is that of the first line of . The number of entries in is therefore equal to the sum of the entries in column of , and the number of entries in is equal to the sum of the entries in row of .
Example
In the above example, the result of applying the Schensted insertion to successively insert 1,3,3,2,2,1,2 into an initially empty tableau results in a tableau , and an additional standard tableau recoding the successive shapes, given by
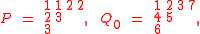
and after replacing the entries 1,2,3,4,5,6,7 in successively by 1,1,1,2,2,3,3 on obtains the pair of semistandard tableaux
Direct definition of the RSK correspondence
The above definition uses the Schensted algorithm, which produces a standard recording tableau , and modifies it to take into account the first line of the two-line array and produce a semistandard recording tableau; this makes the relation to the Robinson–Schensted correspondence evident. It is natural however to simplify the construction by modifying the shape recording part of the algorithm to directly take into account the first line of the two-line array; it is in this form that the algorithm for the RSK correspondence is usually described. This simply means that after every Schensted insertion step, the tableau is extended by adding, as entry of the new square, the -th entry of the first line of , where b is the current size of the tableaux. That this always produces a semistandard tableau follows from the property (first observed by Knuth) that for successive insertions with an identical value in the first line of , each successive square added to the shape is in a column strictly to the right of the previous one.
Here is a detailed example of this construction of both semistandard tableaux. Corresponding to a matrix
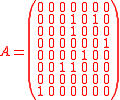
one has the two-line array
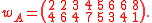
The following table shows the construction of both tableaux for this example
Inserted pair 
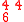
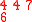
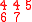
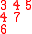
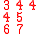
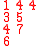
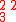
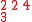
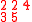
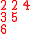
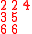
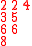
The case of permutation matrices
If
is a permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
then RSK outputs standard Young Tableaux (SYT),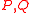
of the same shape 
. Conversely, if 
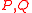are SYT having the same shape 
, then the corresponding matrix 
is a permutation matrix. As a result of this property by simply comparing the cardinalities of the two sets on the two sides of the bijective mapping we get the following corollary:
Corollary 1: For each
we have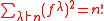 
where
means 
varies over all partitionPartition (number theory)In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
s of
and 
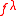is the number of standard Young tableaux of shape 
.
Symmetry
Let
be a matrix with non-negative entries. Suppose the RSK algorithm maps 
to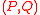 
then the RSK algorithm maps 
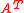to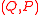 
, where 
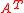is the transpose of 
.
In particular for the case of permutation matrices, one recovers the symmetry of the Robinson–Schensted correspondence:
Theorem 2: If the permutation
corresponds to a triple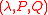 
, then the inverse permutation, 
, corresponds to 
.
This leads to the following relation between the number of involutions on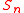
with the number of tableaux that can be formed from 
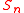(An involution is a permutation that is its own inverse):
Corollary 2: The number of tableaux that can be formed from
is equal to the number of involutions on 
.
Proof: If
is an involution corresponding to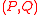 
, then 
corresponds to 
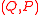; hence 
. Conversely, if 
is any permutation corresponding to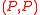 
, then 
also corresponds to 
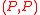; hence 
. So there is a one-one correspondence between involutions 
and tableax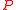 
The number of involutions on
is given by the recurrence:
Where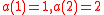
. By solving this recurrence we can get the number of involutions on 
,
Symmetric matrices
Let
and let the RSK algorithm map the matrix 
to the pair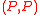 
, where 
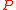is an SSYT of shape 
. Let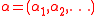 
where the 
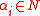and 
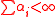. Then the map 
establishes a bijection between symmetric matrices with row(
) 
and SSYT's of type 
.
Cauchy's identity
One has
where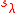
are Schur functionsSchur polynomialIn mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
.
Kostka numbers
Fix partitions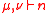
, then
where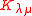
and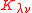 
denote the Kostka numberKostka numberIn mathematics, a Kostka number Kλμ, introduced by , is a non-negative integer depending on two partitions λ and μ, that is equal to the number of semistandard Young tableaux of shape λ and weight μ....
s and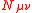
is the number of matrices 
, with non-negative elements, with row row(
) 
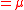and column(
) 
.
-
