
Sandwich theory
Encyclopedia

Sandwich theory describes the behaviour of a beam, plate
Plate theory
In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate...
, or shell which consists of three layers - two facesheets and one core. The most commonly used sandwich theory is linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
and is an extension of first order beam theory. Linear sandwich theory is of importance for the design and analysis of sandwich panels, which are of use in building construction, vehicle construction, airplane construction and refrigeration engineering.
Some advantages of sandwich construction are:
- Sandwich cross sections are compositeComposite materialComposite materials, often shortened to composites or called composition materials, are engineered or naturally occurring materials made from two or more constituent materials with significantly different physical or chemical properties which remain separate and distinct at the macroscopic or...
. They usually consist of a low to moderate stiffnessStiffnessStiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
core which is connected with two stiff exterior face-sheets. The composite has a considerably higher shear stiffness to weight ratio than an equivalent beam made of only the core material or the face-sheet material. The composite also has a high tensile strength to weight ratio. - The high stiffness of the face-sheet leads to a high bending stiffnessBendingIn engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
to weight ratio for the composite.
The behavior of a beam
Beam
Beam may refer to:*Beam , a construction element*Beam , the most extreme width of a nautical vessel, or a point alongside the ship at the mid-point of its length*A narrow, propagating stream of particles or energy:...
with sandwich cross-section under a load differs from a beam with a constant elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
cross section as can be observed in the adjacent figure. If the radius of curvature
Radius of curvature (mathematics)
In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
during bending is small compared to the thickness of a sandwich beam and the strains in the component materials are small, the deformation
Deformation
In materials science, deformation is a change in the shape or size of an object due to an applied force or a change in temperature...
of a sandwich composite beam can be separated into two parts
- deformations due to bending moments or bending deformation, and
- deformations due to transverse forces, also called shear deformation.
Sandwich beam, plate
Plate theory
In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate...
, and shell theories usually assume that the reference stress state is one of zero stress. However, during curing, differences of temperature between the face-sheets persist because of the thermal separation by the core material. These temperature differences, coupled with different linear expansions of the face-sheets, can lead to a bending of the sandwich beam in the direction of the warmer face-sheet. If the bending is constrained during the manufacturing process, residual stress
Residual stress
Residual stresses are stresses that remain after the original cause of the stresses has been removed. They remain along a cross section of the component, even without the external cause. Residual stresses occur for a variety of reasons, including inelastic deformations and heat treatment...
es can develop in the components of a sandwich composite. The superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of a reference stress state on the solutions provided by sandwich theory is possible when the problem is linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
. However, when large elastic deformations and rotations are expected, the initial stress state has to be incorporated directly into the sandwich theory.
Engineering sandwich beam theory
In the engineering theory of sandwich beams, the axial strain is assumed to vary linearly over the cross-section of the beam as in Euler-Bernoulli theory, i.e.,
Therefore the axial stress in the sandwich beam is given by

where
 is the Young's modulus
is the Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
which is a function of the location along the thickness of the beam. The bending moment
Bending Moment
A bending moment exists in a structural element when a moment is applied to the element so that the element bends. Moments and torques are measured as a force multiplied by a distance so they have as unit newton-metres , or pound-foot or foot-pound...
in the beam is then given by

The quantity
 is called the flexural stiffness of the sandwich beam. The shear force
is called the flexural stiffness of the sandwich beam. The shear force  is defined as
is defined as
Using these relations, we can show that the stresses in a sandwich beam with a core of thickness
 and modulus
and modulus  and two facesheets each of thickness
and two facesheets each of thickness  and modulus
and modulus  , are given by
, are given by| Derivation of engineering sandwich beam stresses |
|---|
Since we can write the axial stress as  The equation of equilibrium for a two-dimensional solid is given by  where  is the shear stress is the shear stressShear stress A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section... . Therefore,  where  is a constant of integration. is a constant of integration.Therefore,  Let us assume that there area no shear tractions applied to the top face of the sandwich beam. The shear stress in the top facesheet is given by  At  , ,  implies that implies that  . Then the shear stress at the top of the core, . Then the shear stress at the top of the core,  , is given by , is given by Similarly, the shear stress in the core can be calculated as  The integration constant  is determined from the continuity of shear stress at the interface of the core and the facesheet. Therefore, is determined from the continuity of shear stress at the interface of the core and the facesheet. Therefore, and  |
For a sandwich beam with identical facesheets the value of
 is
is
If
 , then
, then  can be approximated as
can be approximated as
and the stresses in the sandwich beam can be approximated as

If, in addition,
 , then
, then
and the approximate stresses in the beam are

If we assume that the facesheets are thin enough that the stresses may be assumed to be constant through the thickness, we have the approximation
Hence the problem can be split into two parts, one involving only core shear and the other involving only bending stresses in the facesheets.
Bending of a sandwich beam with thin facesheets
The main assumptions of linear sandwich theories of beams with thin facesheets are:- the transverse normal stiffness of the core is infinite, i.e., the core thickness in the z-direction does not change during bending
- the in-plane normal stiffness of the core is small compared to that of the facesheets, i.e., the core does not lengthen or compress in the x-direction
- the facesheets behave according to the Euler-Bernoulli assumptions, i.e., there is no xz-shear in the facesheets and the z-direction thickness of the facesheets does not change
However, the xz shear-stresses in the core are not neglected.
Constitutive assumptions
The constitutive relations relations for two-dimensional orthotropic linear elasticLinear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
materials are

The assumptions of sandwich theory lead to the simplified relations

and

The equilibrium equations in two dimensions are

The assumptions for a sandwich beam and the equilibrium equation imply that

Therefore, for homogeneous facesheets and core, the strains also have the form

Kinematics
Let the sandwich beam be subjected to a bending moment and a shear force
and a shear force  . Let the total deflection of the beam due to these loads be
. Let the total deflection of the beam due to these loads be  . The adjacent figure shows that, for small displacements, the total deflection of the mid-surface of the beam can be expressed as the sum of two deflections, a pure bending deflection
. The adjacent figure shows that, for small displacements, the total deflection of the mid-surface of the beam can be expressed as the sum of two deflections, a pure bending deflection  and a pure shear deflection
and a pure shear deflection  , i.e.,
, i.e.,
From the geometry of the deformation we observe that the engineering shear strain (
 ) in the core is related the effective shear strain in the composite by the relation
) in the core is related the effective shear strain in the composite by the relation
Note the shear strain in the core is larger than the effective shear strain in the composite and that small deformations (
 ) are assumed in deriving the above relation. The effective shear strain in the beam is related to the shear displacement by the relation
) are assumed in deriving the above relation. The effective shear strain in the beam is related to the shear displacement by the relation
The facesheets are assumed to deform in accordance with the assumptions of Euler-Bernoulli beam theory. The total deflection of the facesheets is assumed to be the superposition of the deflections due to bending and that due to core shear. The
 -direction displacements of the facesheets due to bending are given by
-direction displacements of the facesheets due to bending are given by
The displacement of the top facesheet due to shear in the core is

and that of the bottom facesheet is

The normal strains in the two facesheets are given by

Therefore

Stress-displacement relations
The shear stress in the core is given by
or,
The normal stresses in the facesheets are given by

Hence,
Resultant forces and moments
The resultant normal force in a facesheet is defined as
and the resultant moments are defined as

where

Using the expressions for the normal stress in the two facesheets gives
In the core, the resultant moment is

The total bending moment in the beam is

or,
The shear force
 in the core is defined as
in the core is defined aswhere
 is a shear correction coefficient. The shear force in the facesheets can be computed from the bending moments using the relation
is a shear correction coefficient. The shear force in the facesheets can be computed from the bending moments using the relation
or,
For thin facesheets, the shear force in the facesheets is usually ignored.
Bending and shear stiffness
The bending stiffness of the sandwich beam is given by
From the expression for the total bending moment in the beam, we have

For small shear deformations, the above expression can be written as

Therefore, the bending stiffness of the sandwich beam (with
 ) is given by
) is given byand that of the facesheets is
The shear stiffness of the beam is given by

Therefore the shear stiffness of the beam, which is equal to the shear stiffness of the core, is
Relation between bending and shear deflections
A relation can be obtained between the bending and shear deflections by using the continuity of tractions between the core and the facesheets. If we equate the tractions directly we get
At both the facesheet-core interfaces
 but at the top of the core
but at the top of the core  and at the bottom of the core
and at the bottom of the core  . Therefore, traction continuity at
. Therefore, traction continuity at  leads to
leads to
The above relation is rarely used because of the presence of second derivatives of the shear deflection. Instead it is assumed that

which implies that
Governing equations
Using the above definitions, the governing balance equations for the bending moment and shear force are
We can alternatively express the above as two equations that can be solved for
 and
and  as
as
Using the approximations

where
 is the intensity of the applied load on the beam, we have
is the intensity of the applied load on the beam, we haveSeveral techniques may be used to solve this system of two coupled ordinary differential equations given the applied load and the applied bending moment and displacement boundary conditions.
Temperature dependent alternative form of governing equations
Assuming that each partial cross section fulfills Bernoulli's hypothesis, the balance of forces and moments on the deformed sandwich beam element can be used to deduce the bending equation for the sandwich beam.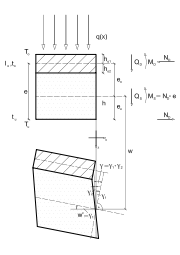
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
:

where
|
 >
>
|-
|

>-
|

>-
|

|-
|

|-
|

|-
|

|-
|

|-
|

|-
|

|-
|

|

>-
|

Superposition of the equations for the facesheets and the core leads to the following equations for the total shear force
 and the total bending moment
and the total bending moment  :
:
We can alternatively express the above as two equations that can be solved for
 and
and  , i.e.,
, i.e.,
Solution approaches

Analytical approach
For simple geometries such as double span beams under uniformly distributed loads, the governing equations can be solved by using appropriate boundary conditions and using the superposition principle. Such results are listed in the standard DIN EN 14509:2006(Table E10.1). Energy methods may also be used to compute solutions directly.Numerical approach
The differential equation of sandwich continuous beams can be solved by the use of numerical methods such as finite differencesFinite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
and finite elements
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
. For finite differences BernerKlaus Berner: Erarbeitung vollständiger Bemessungsgrundlagen im Rahmen bautechnischer Zulassungen für Sandwichbauteile.Fraunhofer IRB Verlag, Stuttgart 2000 (Teil 1). recommends a two-stage approach. After solving the differential equation for the normal forces in the cover sheets for a single span beam under a given load, the energy method can be used to expand the approach for the calculation of multi-span beams. Sandwich continuous beam with flexible cover sheets can also be laid on top of each other when using this technique. However, the cross-section of the beam has to be constant across the spans.
A more specialized approach recommended by Schwarze involves solving for the homogeneous part of the governing equation exactly and for the particular part approximately. Recall that the governing equation for a sandwich beam is

If we define

we get

Schwarze uses the general solution for the homogeneous part of the above equation and a polynomial approximation for the particular solution for sections of a sandwich beam. Interfaces between sections are tied together by matching boundary conditions. This approach has been used in the open source
Open source
The term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
code swe2.
Practical Importance
Results predicted by linear sandwich theory correlate well with the experimentally determined results. The theory is used as a basis for the structural reportStructural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
which is needed for the construction of large industrial and commercial buildings which are clad with sandwich panels . Its use is explicitly demanded for approvals and in the relevant engineering standards.
See also
- BendingBendingIn engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
- Beam theory
- Composite materialComposite materialComposite materials, often shortened to composites or called composition materials, are engineered or naturally occurring materials made from two or more constituent materials with significantly different physical or chemical properties which remain separate and distinct at the macroscopic or...
- Hill yield criteriaHill yield criteriaRodney Hill has developed several yield criteria for anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m...
- Sandwich structured compositeSandwich structured compositeA sandwich-structured composite is a special class of composite materials that is fabricated by attaching two thin but stiff skins to a lightweight but thick core...
- Sandwich plate systemSandwich plate systemSandwich Plate System is a structural composite material composed of steel and polyurethane elastomer.SPS is used in engineered structures including ships, buildings , stadiums ,arenas and bridges and was invented by Dr Stephen Kennedy following his primary research in the field of ice...
- Composite honeycomb
- Timoshenko beam theoryTimoshenko beam theoryThe Timoshenko beam theory was developed by Ukrainian-born scientist Stephen Timoshenko in the beginning of the 20th century. The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behaviour of short beams, sandwich composite beams or...
- Plate theoryPlate theoryIn continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate...
External links
- Institute for Sandwich Technology
- http://www.diabgroup.com/europe/literature/e_pdf_files/man_pdf/sandwich_hb.pdf DIAB Sandwich Handbook
- http://www.swe1.com Programm zur Ermittlung der Schnittgrössen und Spannungen von Sandwich-Wandplatten mit biegeweichen Deckschichten (Open Source)
- http://www.swe2.com Computation of sandwich beams with corrugated faces (Open Source)














