Self-adjoint
Encyclopedia
In mathematics
, an element x of a star-algebra
is self-adjoint if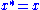
.
A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation. For example, if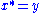
then since 
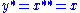in a star-algebra, the set {x,y} is a self-adjoint set even though x and y need not be self-adjoint elements.
In functional analysis
, a linear operator A on a Hilbert space
is called self-adjoint if it is equal to its own adjoint A*. See self-adjoint operator
for a detailed discussion. If the Hilbert space is finite-dimensional and an orthonormal basis
has been chosen, then the operator A is self-adjoint if and only if the matrix
describing A with respect to this basis is Hermitian, i.e. if it is equal to its own conjugate transpose
. Hermitian matrices are also called self-adjoint.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an element x of a star-algebra
Star-algebra
-*-ring:In mathematics, a *-ring is an associative ring with a map * : A → A which is an antiautomorphism and an involution.More precisely, * is required to satisfy the following properties:* ^* = x^* + y^** ^* = y^* x^** 1^* = 1...
is self-adjoint if
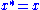.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation. For example, if
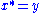then since 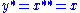in a star-algebra, the set {x,y} is a self-adjoint set even though x and y need not be self-adjoint elements.In functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a linear operator A on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is called self-adjoint if it is equal to its own adjoint A*. See self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
for a detailed discussion. If the Hilbert space is finite-dimensional and an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
has been chosen, then the operator A is self-adjoint if and only if the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
describing A with respect to this basis is Hermitian, i.e. if it is equal to its own conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
. Hermitian matrices are also called self-adjoint.