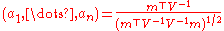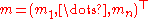Shapiro-Wilk test
Encyclopedia
In statistics
, the Shapiro–Wilk test tests the null hypothesis
that a sample x1, ..., xn came from a normally distributed population. It was published in 1965 by Samuel Shapiro and Martin Wilk
.
The test statistic
is:
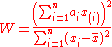
where
The user may reject the null hypothesis if W is too small.
It can be interpreted via a Q-Q plot
.
is less than the chosen alpha level, then the null hypothesis is rejected (i.e. one concludes the data are not from a normally distributed population). If the p-value is greater than the chosen alpha level, then one does not reject the null hypothesis that the data came from a normally distributed population. E.g. for an alpha level of 0.05, a data set with a p-value of 0.32 does not result in rejection of the hypothesis that the data are from a normally distributed population.http://www.jmp.com/support/faq/jmp2085.shtml
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Shapiro–Wilk test tests the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that a sample x1, ..., xn came from a normally distributed population. It was published in 1965 by Samuel Shapiro and Martin Wilk
Martin Wilk
Martin Bradbury Wilk, is a Canadian statistician, academic, and the former Chief Statistician of Canada. In 1965, together with Samuel Shapiro, he developed the Shapiro-Wilk test which can indicate whether a sample of numbers would be unusual if it came from a Gaussian distribution.Born in...
.
The test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
is:
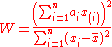
where
- x(i) (with parentheses enclosing the subscript index i) is the ith order statisticOrder statisticIn statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....
, i.e., the ith-smallest number in the sample; = (x1 + ... + xn) / n is the sample mean; - the constants ai are given by
- where
- and m1, ..., mn are the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s of the order statisticOrder statisticIn statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....
s of independent and identically-distributed random variables sampled from the standard normal distribution, and V is the covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of those order statistics.
The user may reject the null hypothesis if W is too small.
It can be interpreted via a Q-Q plot
Q-Q plot
In statistics, a Q-Q plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles are chosen...
.
Interpretation
Recalling that the null hypothesis is that the population is normally distributed, if the p-valueP-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
is less than the chosen alpha level, then the null hypothesis is rejected (i.e. one concludes the data are not from a normally distributed population). If the p-value is greater than the chosen alpha level, then one does not reject the null hypothesis that the data came from a normally distributed population. E.g. for an alpha level of 0.05, a data set with a p-value of 0.32 does not result in rejection of the hypothesis that the data are from a normally distributed population.http://www.jmp.com/support/faq/jmp2085.shtml
See also
- Anderson–Darling test
- Kolmogorov–Smirnov test
- Cramér–von Mises criterion
- Normal probability plotNormal probability plotThe normal probability plot is a graphical technique for normality testing: assessing whether or not a data set is approximately normally distributed....
- Q-Q plotQ-Q plotIn statistics, a Q-Q plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles are chosen...