The Siamese method, or De la Loubère method, is a simple method to construct any size of n-odd magic squares (i.e. number squares in which the sums of all rows, columns and diagonals are identical). The method was brought to France

France

The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...

 in 1688 by the French mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

 and diplomat

Diplomat

A diplomat is a person appointed by a state to conduct diplomacy with another state or international organization. The main functions of diplomats revolve around the representation and protection of the interests and nationals of the sending state, as well as the promotion of information and...

 Simon de la Loubère

Simon de la Loubère

Simon de la Loubère was a French diplomat, writer, mathematician and poet.-Mission to Siam:Simon de la Loubère led an embassy to Siam in 1687 . The embassy, composed of five warships, arrived in Bangkok in October 1687 and was received by Ok-khun Chamnan...

, as he was returning from his 1687 embassy to the kingdom of Siam. The Siamese method makes the creation of magic square

Magic square

In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...

s straightforward.

Publication

De la Loubère published his findings in his book A new historical relation of the kingdom of Siam (Du Royaume de Siam, 1693), under the chapter entitled The problem of the magical square according to the Indians.
Although the method is generally qualified as "Siamese", which refers to de la Loubère's travel to the country of Siam, de la Loubère himself learnt it from a Frenchman named M.Vincent (a doctor, who had first travelled to Persia and then to Siam, and was returning to France with the de la Loubère embassy), who himself had learnt it in the city of Surat

Surat

Surat , also known as Suryapur, is the commercial capital city of the Indian state of Gujarat. Surat is India's Eighth most populous city and Ninth-most populous urban agglomeration. It is also administrative capital of Surat district and one of the fastest growing cities in India. The city proper...

 in India

India

India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...

:

The method

The method was surprising in its effectiveness and simplicity:
First, an arithmetic progression

Arithmetic progression

In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...

 has to be chosen (such as the simple progression 1,2,3,4,5,6,7,8,9 for a square with three rows and columns (the Lo Shu square

Lo Shu Square

Lo Shu Square |Luo ]] Book/Scroll) or the Nine Halls Diagram , is the unique normal magic square of order three. Lo Shu is part of the legacy of the most ancient Chinese mathematical and divinatory traditions, and is an important emblem in Feng Shui , the art of geomancy concerned with the...

)).

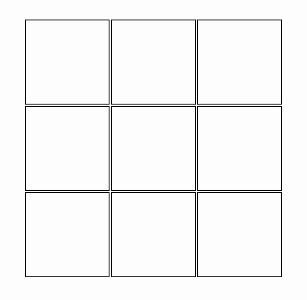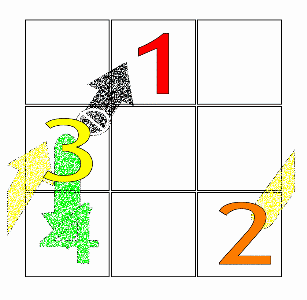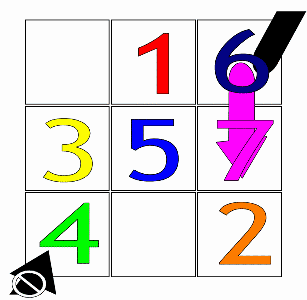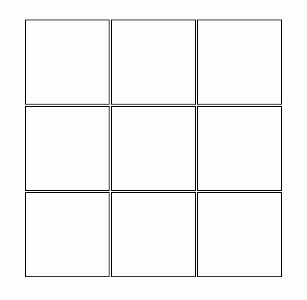
Then, starting from the central box of the first row with the number 1 (or the first number of any arithmetic progression), the fundamental movement for filling the boxes is diagonally up and right (↗), one step at a time. When a move would leave the square, it is wrapped around to the last row or first column, respectively.

If a filled box is encountered, one moves vertically down one box (↓) instead, then continuing as before.

Order-3 magic squares

step 1 1 . .

step 2 1 . 2

step 3 1 3 2

step 4 1 3 4 2

step 5 1 6 3 5 4 2

step 6 1 6 3 5 7 4 2

step 7 8 1 6 3 5 7 4 2

step 8 8 1 6 3 5 7 4 9 2

Order-5 magic squares

Step 1 1 . . . .

Step 2 1 . . . 3 . 2

Step 3 1 5 4 . 3 2

Step 4 1 8 5 7 4 6 . 3 2

Step 5 1 8 15 5 7 14 4 6 13 10 12 3 11 2 9

Step 6 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9

Other sizes

Any n-odd square ("odd-order square") can be thus built into a magic square. The Siamese method does not work however for n-even squares ("even-order squares", such as 2 rows/ 2 columns, 4 rows/ 4 columns etc...).

Order 3 8 1 6 3 5 7 4 9 2

Order 5 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9

Order 9 47 58 69 80 1 12 23 34 45 57 68 79 9 11 22 33 44 46 67 78 8 10 21 32 43 54 56 77 7 18 20 31 42 53 55 66 6 17 19 30 41 52 63 65 76 16 27 29 40 51 62 64 75 5 26 28 39 50 61 72 74 4 15 36 38 49 60 71 73 3 14 25 37 48 59 70 81 2 13 24 35

Other values

Any sequence of numbers can be used, provided they form an arithmetic progression

Arithmetic progression

In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...

 (i.e. the difference of any two successive members of the sequence is a constant). Also, any starting number is possible. For example the following sequence can be used to form an order 3 magic square according to the Siamese method (9 boxes): 5, 10, 15, 20, 25, 30, 35, 40, 45 (the magic sum gives 75, for all rows, columns and diagonals).

Order 3
40	5	30
15	25	35
20	45	10

Other starting points

It is possible not to start the arithmetic progression from the middle of the top row, but then only the row and column sums will be identical and result in a magic sum, whereas the diagonal sums will differ. The result will thus not be a true magic square:

Order 3
500	700	300
900	200	400
100	600	800

Rotations and reflexions

Numerous other magic squares can be deduced from the above by simple rotations and reflections

Reflection (mathematics)

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

.

Variations

A slightly more complicated variation of this method exists in which the first number is placed in the box just above the center box. The fundamental movement for filling the boxes remains up and right (↗), one step at a time. However, if a filled box is encountered, one moves vertically up two boxes instead, then continuing as before.

Order 5
23	6	19	2	15
10	18	1	14	22
17	5	13	21	9
4	12	25	8	16
11	24	7	20	3

Numerous variants can be obtained by simple rotations and reflections. The next square is equivalent to the above (a simple reflexion): the first number is placed in the box just below the center box. The fundamental movement for filling the boxes then becomes diagonally down and right (↘), one step at a time. If a filled box is encountered, one moves vertically down two boxes instead, then continuing as before.

Order 5
11	24	7	20	3
4	12	25	8	16
17	5	13	21	9
10	18	1	14	22
23	6	19	2	15

These variations, although not quite as simple as the basic Siamese method, are equivalent to the methods developed by earlier European scholars, Johann Faulhaber

Johann Faulhaber

Johann Faulhaber was a German mathematician.Born in Ulm, Faulhaber trained as a weaver and later took the role of a surveyor of the city of Ulm. He collaborated with Johannes Kepler and Ludolph van Ceulen...

 (1580–1635) and Claude Gaspard Bachet de Méziriac

Claude Gaspard Bachet de Méziriac

Claude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse.Bachet was a pupil of the Jesuit mathematician Jacques de Billy at the Jesuit College in Rheims...

(1581–1638), and allowed to create magic squares similar to theirs.