
Smith-Volterra-Cantor set
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Smith–Volterra–Cantor set (SVC), fat Cantor set, or ε-Cantor set is an example of a set of points on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R that is nowhere dense (in particular it contains no interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s), yet has positive measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
. The Smith–Volterra–Cantor set is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Henry Smith
Henry John Stephen Smith
Henry John Stephen Smith was a mathematician remembered for his work in elementary divisors, quadratic forms, and Smith–Minkowski–Siegel mass formula in number theory...
, Vito Volterra
Vito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
and Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
.
Construction
Similar to the construction of the Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, the Smith–Volterra–Cantor set is constructed by removing certain intervals from the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1].
The process begins by removing the middle 1/4 from the interval [0, 1] (the same as removing 1/8 on either side of the middle point at 1/2) so the remaining set is
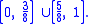
The following steps consist of removing subintervals of width 1/22n from the middle of each of the 2n−1 remaining intervals. So for the second step the intervals (5/32, 7/32) and (25/32, 27/32) are removed, leaving
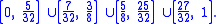
Continuing indefinitely with this removal, the Smith–Volterra–Cantor set is then the set of points that are never removed. The image below shows the initial set and five iterations of this process.

Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, where the proportion removed from each interval remains constant. Thus, the former has positive measure, while the latter zero measure.
Properties
By construction, the Smith–Volterra–Cantor set contains no intervals and therefore has empty interior. It is also the intersection of a sequence of closed sets, which means that it is closed.During the process, intervals of total length
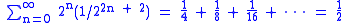
are removed from [0, 1], showing that the set of the remaining points has a positive measure of 1/2. This makes the Smith-Volterra-Cantor set an example of a closed set whose boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
has positive Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
Other fat Cantor sets
In general, one can remove rn from each remaining subinterval at the n-th step of the algorithm, and end up with a Cantor-like set. The resulting set will have positive measure if and only if the sum of the sequence is less than the measure of the initial interval.See also
- The SVC is used in the construction of Volterra's functionVolterra's functionIn mathematics, Volterra's function, named for Vito Volterra, is a real-valued function V defined on the real line R with the following curious combination of properties:* V is differentiable everywhere...
(see external link). - The SVC is an example of a compact set that is not Jordan measurable, see Jordan measure#Extension to more complicated sets.
- The indicator function of the SVC is an example of a bounded function that is not Riemann integrable on (0,1) and moreover, is not equal almost everywhere to a Riemann integrable function, see Riemann integral#Examples.
External links
- Wrestling with the Fundamental Theorem of Calculus: Volterra's function, talk by David Marius BressoudDavid BressoudDavid Marius Bressoud is an American mathematician who works in number theory, combinatorics, and special functions...

