
Specker sequence
Encyclopedia
In computability theory
, a Specker sequence is a computable
, strictly increasing, bounded sequence of rational numbers whose supremum
is not a computable real number. The first example of such a sequence was constructed by Ernst Specker
in 1949.
The existence of Specker sequences has consequences for computable analysis
. The fact that such sequences exist means that the collection of all computable real numbers does not satisfy the least upper bound principle of real analysis. A common way to resolve this difficulty is to consider only sequences that are accompanied by a modulus of convergence
; no Specker sequence has a computable modulus of convergence.
The least upper bound principle has also been analyzed in the program of reverse mathematics
, where the exact strength of this principle has been determined. In the terminology of that program, the least upper bound principle is equivalent to ACA0 over RCA0.
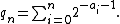
It is clear that each qn is nonnegative and rational, and that the sequence qn is strictly increasing. Moreover, because ai has no repetition, it is possible to estimate each qn against the series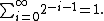
Thus the sequence (qn) is bounded above by 1. Classically, this means that qn has a supremum x.
It is shown that x is not a computable real number. The proof uses a particular fact about computable real numbers. If x were computable then there would be a computable function r(n) such that |qj - qi| < 1/n for all i,j > r(n). To compute r, compare the binary expansion of x with the binary expansion of qi for larger and larger values of i. The definition of qi causes a single binary digit to go from 0 to 1 each time i increases by 1. Thus there will be some n where a large enough initial segment of x has already been determined by qn that no additional binary digits in that segment could ever be turned on, which leads to an estimate on the distance between qi and qj for i,j > n.
If any such a function r were computable, it would lead to a decision procedure for A, as follows. Given an input k, compute r(2k+1). Note that if k were to appear in the sequence (ai), this would cause the sequence (qi) to increase by 2-k-1, but this cannot happen once all the elements of (qi) are within 2-k-1 of each other. Thus, if k is going to be enumerated into ai, it must be enumerated for a value of i less than r(2k+1). This leaves a finite number of possible places where k could be enumerated. To complete the decision procedure, check these in an effective manner and the return 0 or 1 depending on whether k is found.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, a Specker sequence is a computable
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
, strictly increasing, bounded sequence of rational numbers whose supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is not a computable real number. The first example of such a sequence was constructed by Ernst Specker
Ernst Specker
Ernst P. Specker is a Swiss mathematician. Much of his most influential work has been on Quine’s New Foundations, a set theory with a universal set, but he is most famous for the Kochen–Specker theorem in quantum mechanics, showing that certain types of hidden variable theories are impossible...
in 1949.
The existence of Specker sequences has consequences for computable analysis
Computable analysis
In mathematics, computable analysis is the study of which parts of real analysis and functional analysis can be carried out in a computable manner. It is closely related to constructive analysis.- Basic results :...
. The fact that such sequences exist means that the collection of all computable real numbers does not satisfy the least upper bound principle of real analysis. A common way to resolve this difficulty is to consider only sequences that are accompanied by a modulus of convergence
Modulus of convergence
In real analysis, a branch of mathematics, a modulus of convergence is a function that tells how quickly a convergent sequence converges. These moduli are often employed in the study of computable analysis and constructive mathematics....
; no Specker sequence has a computable modulus of convergence.
The least upper bound principle has also been analyzed in the program of reverse mathematics
Reverse mathematics
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
, where the exact strength of this principle has been determined. In the terminology of that program, the least upper bound principle is equivalent to ACA0 over RCA0.
Construction
The following construction is described by Kushner (1984). Let A be any recursively enumerable set of natural numbers that is not decidable, and let (ai) be a computable enumeration of A without repetition. Define a sequence (qn) of rational numbers with the rule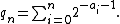
It is clear that each qn is nonnegative and rational, and that the sequence qn is strictly increasing. Moreover, because ai has no repetition, it is possible to estimate each qn against the series
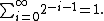
Thus the sequence (qn) is bounded above by 1. Classically, this means that qn has a supremum x.
It is shown that x is not a computable real number. The proof uses a particular fact about computable real numbers. If x were computable then there would be a computable function r(n) such that |qj - qi| < 1/n for all i,j > r(n). To compute r, compare the binary expansion of x with the binary expansion of qi for larger and larger values of i. The definition of qi causes a single binary digit to go from 0 to 1 each time i increases by 1. Thus there will be some n where a large enough initial segment of x has already been determined by qn that no additional binary digits in that segment could ever be turned on, which leads to an estimate on the distance between qi and qj for i,j > n.
If any such a function r were computable, it would lead to a decision procedure for A, as follows. Given an input k, compute r(2k+1). Note that if k were to appear in the sequence (ai), this would cause the sequence (qi) to increase by 2-k-1, but this cannot happen once all the elements of (qi) are within 2-k-1 of each other. Thus, if k is going to be enumerated into ai, it must be enumerated for a value of i less than r(2k+1). This leaves a finite number of possible places where k could be enumerated. To complete the decision procedure, check these in an effective manner and the return 0 or 1 depending on whether k is found.

