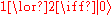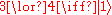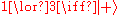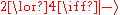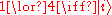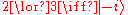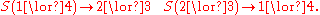Spekkens Toy Model
Encyclopedia
The Spekkens toy model is a conceptually simple model, introduced by Robert Spekkens in 2004, to argue in favour of the epistemic view of quantum mechanics
. The model is based on a foundational principle: "If one has maximal knowledge, then for every system, at every time, the amount of knowledge one possesses about the ontic
state of the system at that time must equal the amount of knowledge one lacks." This is called the "knowledge balance principle." Within the bounds of this model, many phenomena typically associated with strictly quantum mechanical effects are present. These include (but are not limited to) entanglement
, noncommutativity of measurements, teleportation
, interference
, no cloning
and no broadcasting
theorems, and unsharp measurements. Much of the mathematics
associated with quantum theory has strong analogues inside the toy model, such as the Bloch sphere
and similar forms of transformations. The model is not, however, a restriction of quantum mechanics, as there are effects in the model not present in quantum theory.
s and philosophers have been attempting to explain the physical meaning of quantum states. The argument is typically one between two fundamentally opposed views: the ontic
view, which describes quantum states as states of physical reality
, and the epistemic view, which describes quantum states as states of our incomplete knowledge about a system. Both views have had strong support over the years; notably, the ontic view was supported by Heisenberg
and Schrödinger
and the epistemic view by Einstein
. The majority of 20th century quantum physics was dominated by the ontic view, and it remains the generally accepted view by physicists today. There is, however, a substantial subset of physicists who take the epistemic view. Both views have issues associated with them, as both contradict physical intuition
in many cases, and neither has been conclusively proven to be the superior viewpoint.
The Spekkens toy model is designed to argue in favour of the epistemic viewpoint. It is, by construction, an epistemic model. The knowledge balance principle of the model ensures that any measurement done on a system within it gives incomplete knowledge of the system, and thus the observable states of the system are epistemic. This model also implicitly assumes that there is an ontic state which the system is in at any given time, but simply that we are unable to observe it. The model can not be used to derive quantum mechanics, as there are fundamental differences between the model and quantum theory. In particular, the model is one of local and noncontextual variable
s, which Bell's theorem
tells us cannot ever reproduce all the predictions of quantum mechanics. The toy model does, however, reproduce a number of strange quantum effects, and it does so from a strictly epistemic perspective; as such, it can be interpreted as strong evidence in favour of the epistemic view.
must be carefully defined for this principle to have any meaning. To do this, the concept of a canonical set of yes or no questions is defined as the minimum number of questions needed. For example, for a system with 4 states, one can ask "Is the system in state 1?", "Is the system in state 2?" and "Is the system in state 3?" which would determine the state of the system (state 4 being the case if all three questions were answered "No."). However, one could also ask "Is the system in either state 1 or state 2?" and "Is the system in either state 1 or state 3?", which would also uniquely determine the state, and has only two questions in the set. This set of questions is not unique, however this is clearly the minimum number of questions needed to definitively determine the state, so for a system with 4 states, the number of questions in a canonical
set is two. As such, in this case, the knowledge balance principle insists that the maximum number of questions in a canonical set that one can have answered at any given time is one, such that the amount of knowledge is equal to the amount of ignorance.
It is also assumed in the model that it is always possible to saturate the inequality, i.e. to have knowledge of the system exactly equal to that which is lacked, and thus at least two questions must be in the canonical set. Since no question is allowed to exactly specify the state of the system, the number of possible ontic states must be at least 4 (if it were less than 4, the model would be trivial, since any question that could be asked may return an answer specifying the exact state of the system, thus no question can be asked). Since a system with four states (described above) exists, it is referred to as an elementary
system. The model then also assumes that every system is built out of these elementary systems, and that each subsystem of any system also obeys the knowledge balance principle.
ped to six qubit
states in a natural manner;
Under this mapping, it is clear that two states of knowledge in the toy theory correspond to two orthogonal
states for the qubit if and only if they share no ontic states in common. This mapping also gives analogues
in the toy model to quantum fidelity
, compatibility
, convex combination
s of states and coherent superposition
, and can be mapped to the Bloch sphere
in the natural fashion. However, the analogy breaks down to a degree when considering coherent superposition, as one of the forms of the coherent superposition in the toy model returns a state which is orthogonal to what is expected with the corresponding superposition in the quantum model, and this can be shown to be an intrinsic difference between the two systems. This reinforces the earlier point that this model is not a restricted version of quantum mechanics, but instead a separate model which mimics quantum properties.
Considering again the analogy between the epistemic states of this model and the qubit states on the Bloch Sphere, these transformations consist of the typical allowed permutation
s of the six analogous states, as well as a set of permutations that are forbidden in the continuous qubit model. These are transformations such as (12)(3)(4) which correspond to antiunitary maps on Hilbert space
. These are not allowed in a continuous model, however in this discrete system they arise as natural transformations. There is however an analogy to a characteristically quantum phenomenon, that no allowed transformation functions as a universal state
inverter
. In this case, this means that there is no single transformation S with the properties
s (measurements which cause the system after the measurement to be consistent with the results of the measurement) are considered. As such, only measurements which distinguish between valid epistemic states are allowed. For instance, we could measure whether the system is in states 1 or 2, 1 or 3, or 1 or 4, corresponding to 1 ∨ 2, 1 ∨ 3, and 1 ∨ 4. Once the measurement has been done, one's state of knowledge about the system in question is updated; specifically, if one measured the system in the state 2 ∨ 4, then the system would now be known to be in the ontic state 2 or the ontic state 4.
Before a measurement is done on a system, it has a definite ontic state, in the case of an elementary system 1, 2, 3 or 4. If the initial ontic state of a system is 1, and one measured the state of the system with respect to the {1 ∨ 3, 2∨ 4} basis, then one would measure the state 1 ∨ 3. Another measurement done in this basis would produce the same result. However, the underlying ontic state of the system can be changed by such a measurement, to either the state 1 or the state 3. This reflects the nature of measurement in quantum theory.
Measurements done on a system in the toy model
are non-commutative, as is the case for quantum measurements. This is due to the above fact, that a measurement can change the underlying ontic state of the system. For example, if one measures a system in the state 1 ∨ 3 in the {1 ∨ 3, 2 ∨ 4} basis, then one obtains the state 1 ∨ 3 with certainty. However, if one first measures the system in the {1 ∨ 2, 3 ∨ 4} basis, then in the {1 ∨ 3, 2 ∨ 4} basis, then the final state of the system is uncertain, prior to the measurement.
The nature of measurements and of the coherent superposition in this theory also gives rise to the quantum phenomenon of interference. When two states are mixed by a coherent superposition, the result is a sampling of the ontic states from both, rather than the typical "and" or "or". This is one of the most important results of this model, as interference is often seen as evidence against the epistemic view. This model indicates that it can arise from a strictly epistemic system.
states, corresponding to the combinations of the numbers 1 through 4 with 1 through 4 (i.e. the system can be in the state (1,1), (1,2), etc.) The epistemic state of the system is limited by the knowledge balance principle once again. Now however, not only does it restrict the knowledge of the system as a whole, but also of both of the constituent subsystems. Two types of systems of maximal knowledge arise as a result. The first of these corresponds to having maximal knowledge of both subsystems; for example, that the first subsystem is in the state 1 ∨ 3 and the second is in the state 3 ∨ 4, meaning that the system as a whole is in one of the states (1,3), (1,4), (3,3) or (3,4). In this case, nothing is known about the correspondence between the two systems. The second is more interesting, corresponding to having no knowledge about either system individually, but having maximal knowledge about their interaction. For example, one could know that the ontic state of the system is one of (1,1), (2,2), (3,4) or (4,3). Here nothing is known about the state of either individual system, but knowledge of one system gives knowledge of the other. This corresponds to the entangling
of particles in quantum theory
.
It is possible to consider valid transformations on the states of a group of elementary systems, although the mathematics
of such an analysis is more complicated than the case for a single system. Transformations consisting of a valid transformation on each state acting independently are always valid. In the case of a two system model, there is also a transformation which is analogous to the c-not
operator on qubits. Furthermore, within the bounds of the model it is possible to prove no-cloning and no-broadcasting theorems, reproducing a fair deal of the mechanics of quantum information theory.
The monogamy
of pure entanglement also has a strong analogue within the toy model, as a group of three or more systems in which knowledge of one system would grant knowledge of the others would break the knowledge balance principle. An analogy of quantum teleportation
also exists in the model, as well as a number of important quantum phenomena.
Currently, there is work being done to reproduce quantum formalism
from information-theoretic axiom
s. Although the model itself differs in many respects from quantum theory, it reproduces a number of effects which are considered to be overwhelmingly quantum. As such, the underlying principle, that quantum states are states of incomplete knowledge
, may offer some hints as to how to proceed in this manner, and may lend hope to those pursuing this goal.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The model is based on a foundational principle: "If one has maximal knowledge, then for every system, at every time, the amount of knowledge one possesses about the ontic
Ontic
In philosophy, ontic is physical, real or factual existence."Ontic" describes what is there, as opposed to the nature or properties of that being...
state of the system at that time must equal the amount of knowledge one lacks." This is called the "knowledge balance principle." Within the bounds of this model, many phenomena typically associated with strictly quantum mechanical effects are present. These include (but are not limited to) entanglement
Entanglement
Entanglement may refer to:* Quantum entanglement* Orientation entanglement* Entanglement * Entanglement of polymer chains, see Reptation* Wire entanglement...
, noncommutativity of measurements, teleportation
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
, interference
Interference
In physics, interference is a phenomenon in which two waves superpose to form a resultant wave of greater or lower amplitude. Interference usually refers to the interaction of waves that are correlated or coherent with each other, either because they come from the same source or because they have...
, no cloning
Cloning
Cloning in biology is the process of producing similar populations of genetically identical individuals that occurs in nature when organisms such as bacteria, insects or plants reproduce asexually. Cloning in biotechnology refers to processes used to create copies of DNA fragments , cells , or...
and no broadcasting
Broadcasting
Broadcasting is the distribution of audio and video content to a dispersed audience via any audio visual medium. Receiving parties may include the general public or a relatively large subset of thereof...
theorems, and unsharp measurements. Much of the mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
associated with quantum theory has strong analogues inside the toy model, such as the Bloch sphere
Bloch sphere
In quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system , named after the physicist Felix Bloch....
and similar forms of transformations. The model is not, however, a restriction of quantum mechanics, as there are effects in the model not present in quantum theory.
Background
For nearly a century, physicistPhysicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
s and philosophers have been attempting to explain the physical meaning of quantum states. The argument is typically one between two fundamentally opposed views: the ontic
Ontic
In philosophy, ontic is physical, real or factual existence."Ontic" describes what is there, as opposed to the nature or properties of that being...
view, which describes quantum states as states of physical reality
Reality
In philosophy, reality is the state of things as they actually exist, rather than as they may appear or might be imagined. In a wider definition, reality includes everything that is and has been, whether or not it is observable or comprehensible...
, and the epistemic view, which describes quantum states as states of our incomplete knowledge about a system. Both views have had strong support over the years; notably, the ontic view was supported by Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
and Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
and the epistemic view by Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
. The majority of 20th century quantum physics was dominated by the ontic view, and it remains the generally accepted view by physicists today. There is, however, a substantial subset of physicists who take the epistemic view. Both views have issues associated with them, as both contradict physical intuition
Intuition (knowledge)
Intuition is the ability to acquire knowledge without inference or the use of reason. "The word 'intuition' comes from the Latin word 'intueri', which is often roughly translated as meaning 'to look inside'’ or 'to contemplate'." Intuition provides us with beliefs that we cannot necessarily justify...
in many cases, and neither has been conclusively proven to be the superior viewpoint.
The Spekkens toy model is designed to argue in favour of the epistemic viewpoint. It is, by construction, an epistemic model. The knowledge balance principle of the model ensures that any measurement done on a system within it gives incomplete knowledge of the system, and thus the observable states of the system are epistemic. This model also implicitly assumes that there is an ontic state which the system is in at any given time, but simply that we are unable to observe it. The model can not be used to derive quantum mechanics, as there are fundamental differences between the model and quantum theory. In particular, the model is one of local and noncontextual variable
Variable
Variable may refer to:* Variable , a logical set of attributes* Variable , a symbol that represents a quantity in an algebraic expression....
s, which Bell's theorem
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
tells us cannot ever reproduce all the predictions of quantum mechanics. The toy model does, however, reproduce a number of strange quantum effects, and it does so from a strictly epistemic perspective; as such, it can be interpreted as strong evidence in favour of the epistemic view.
The model
The Spekkens toy model is based on the knowledge balance principle, stated in the introduction. However, the "knowledge" one can possess about a systemSystem
System is a set of interacting or interdependent components forming an integrated whole....
must be carefully defined for this principle to have any meaning. To do this, the concept of a canonical set of yes or no questions is defined as the minimum number of questions needed. For example, for a system with 4 states, one can ask "Is the system in state 1?", "Is the system in state 2?" and "Is the system in state 3?" which would determine the state of the system (state 4 being the case if all three questions were answered "No."). However, one could also ask "Is the system in either state 1 or state 2?" and "Is the system in either state 1 or state 3?", which would also uniquely determine the state, and has only two questions in the set. This set of questions is not unique, however this is clearly the minimum number of questions needed to definitively determine the state, so for a system with 4 states, the number of questions in a canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
set is two. As such, in this case, the knowledge balance principle insists that the maximum number of questions in a canonical set that one can have answered at any given time is one, such that the amount of knowledge is equal to the amount of ignorance.
It is also assumed in the model that it is always possible to saturate the inequality, i.e. to have knowledge of the system exactly equal to that which is lacked, and thus at least two questions must be in the canonical set. Since no question is allowed to exactly specify the state of the system, the number of possible ontic states must be at least 4 (if it were less than 4, the model would be trivial, since any question that could be asked may return an answer specifying the exact state of the system, thus no question can be asked). Since a system with four states (described above) exists, it is referred to as an elementary
Elementary
Elementary may refer to:*Elementary or Primary education, the first years of formal, structured education that occur during childhood*Elementary school, a school providing elementary or primary education*Elementary , 2007...
system. The model then also assumes that every system is built out of these elementary systems, and that each subsystem of any system also obeys the knowledge balance principle.
Elementary systems
For an elementary system, let 1 ∨ 2 represent the state of knowledge "The system is in the state one or the state 2." Under this model, there are six states of maximal knowledge that can be obtained: 1 ∨ 2, 1 ∨ 3, 1 ∨ 4, 2 ∨ 3, 2 ∨ 4 and 3 ∨ 4. There is also a single state less than maximal knowledge, corresponding to 1 ∨ 2 ∨ 3 ∨ 4. These can be mapMap
A map is a visual representation of an area—a symbolic depiction highlighting relationships between elements of that space such as objects, regions, and themes....
ped to six qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
states in a natural manner;
-
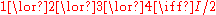 .
.
Under this mapping, it is clear that two states of knowledge in the toy theory correspond to two orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
states for the qubit if and only if they share no ontic states in common. This mapping also gives analogues
Analogy
Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...
in the toy model to quantum fidelity
Fidelity
"Fidelity" is the quality of being faithful or loyal. Its original meaning regarded duty to a lord or a king, in a broader sense than the related concept of fealty. Both derive from the Latin word fidēlis, meaning "faithful or loyal"....
, compatibility
Compatibility
Compatibility may refer to:* Astrological compatibility* Compatibilism – a philosophical position* Compatibility * Compatibility * Compatibility * Electromagnetic compatibility* Interpersonal compatibility-Computing:...
, convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s of states and coherent superposition
Superposition
Superposition can refer to:* The superposition principle in physics, mathematics, and engineering, describes the overlapping of waves. Particular applications include :** Quantum superposition, in quantum physics** Superposition theorem, in electronics....
, and can be mapped to the Bloch sphere
Bloch sphere
In quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system , named after the physicist Felix Bloch....
in the natural fashion. However, the analogy breaks down to a degree when considering coherent superposition, as one of the forms of the coherent superposition in the toy model returns a state which is orthogonal to what is expected with the corresponding superposition in the quantum model, and this can be shown to be an intrinsic difference between the two systems. This reinforces the earlier point that this model is not a restricted version of quantum mechanics, but instead a separate model which mimics quantum properties.
Transformations
The only transformations on the ontic state of the system which respect the knowledge balance principle are permutations of the four ontic states. These map valid epistemic states to other valid epistemic states, for instanceConsidering again the analogy between the epistemic states of this model and the qubit states on the Bloch Sphere, these transformations consist of the typical allowed permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of the six analogous states, as well as a set of permutations that are forbidden in the continuous qubit model. These are transformations such as (12)(3)(4) which correspond to antiunitary maps on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. These are not allowed in a continuous model, however in this discrete system they arise as natural transformations. There is however an analogy to a characteristically quantum phenomenon, that no allowed transformation functions as a universal state
Universal state
Universal state may refer to*Universal state , as used in reference to A Study of History, a work by historian Toynbee.*Universal state , a concept in the study of computational complexity...
inverter
Inverter
Inverter may refer to* Inverter , a device that converts direct current to alternating current** Inverter , an air conditioner that can continuously regulate its output by altering the compressor speed in response to cooling demand** Uninterruptible power supply, which often are based on an...
. In this case, this means that there is no single transformation S with the properties
Measurements
In the theory, only reproducible measurementMeasurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
s (measurements which cause the system after the measurement to be consistent with the results of the measurement) are considered. As such, only measurements which distinguish between valid epistemic states are allowed. For instance, we could measure whether the system is in states 1 or 2, 1 or 3, or 1 or 4, corresponding to 1 ∨ 2, 1 ∨ 3, and 1 ∨ 4. Once the measurement has been done, one's state of knowledge about the system in question is updated; specifically, if one measured the system in the state 2 ∨ 4, then the system would now be known to be in the ontic state 2 or the ontic state 4.
Before a measurement is done on a system, it has a definite ontic state, in the case of an elementary system 1, 2, 3 or 4. If the initial ontic state of a system is 1, and one measured the state of the system with respect to the {1 ∨ 3, 2∨ 4} basis, then one would measure the state 1 ∨ 3. Another measurement done in this basis would produce the same result. However, the underlying ontic state of the system can be changed by such a measurement, to either the state 1 or the state 3. This reflects the nature of measurement in quantum theory.
Measurements done on a system in the toy model
Toy model
In physics, a toy model is a simplified set of objects and equations relating them that can nevertheless be used to understand a mechanism that is also useful in the full, non-simplified theory....
are non-commutative, as is the case for quantum measurements. This is due to the above fact, that a measurement can change the underlying ontic state of the system. For example, if one measures a system in the state 1 ∨ 3 in the {1 ∨ 3, 2 ∨ 4} basis, then one obtains the state 1 ∨ 3 with certainty. However, if one first measures the system in the {1 ∨ 2, 3 ∨ 4} basis, then in the {1 ∨ 3, 2 ∨ 4} basis, then the final state of the system is uncertain, prior to the measurement.
The nature of measurements and of the coherent superposition in this theory also gives rise to the quantum phenomenon of interference. When two states are mixed by a coherent superposition, the result is a sampling of the ontic states from both, rather than the typical "and" or "or". This is one of the most important results of this model, as interference is often seen as evidence against the epistemic view. This model indicates that it can arise from a strictly epistemic system.
Groups of elementary systems
A pair of elementary systems has 16 combined onticOntic
In philosophy, ontic is physical, real or factual existence."Ontic" describes what is there, as opposed to the nature or properties of that being...
states, corresponding to the combinations of the numbers 1 through 4 with 1 through 4 (i.e. the system can be in the state (1,1), (1,2), etc.) The epistemic state of the system is limited by the knowledge balance principle once again. Now however, not only does it restrict the knowledge of the system as a whole, but also of both of the constituent subsystems. Two types of systems of maximal knowledge arise as a result. The first of these corresponds to having maximal knowledge of both subsystems; for example, that the first subsystem is in the state 1 ∨ 3 and the second is in the state 3 ∨ 4, meaning that the system as a whole is in one of the states (1,3), (1,4), (3,3) or (3,4). In this case, nothing is known about the correspondence between the two systems. The second is more interesting, corresponding to having no knowledge about either system individually, but having maximal knowledge about their interaction. For example, one could know that the ontic state of the system is one of (1,1), (2,2), (3,4) or (4,3). Here nothing is known about the state of either individual system, but knowledge of one system gives knowledge of the other. This corresponds to the entangling
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
of particles in quantum theory
Quantum theory
Quantum theory may mean:In science:*Quantum mechanics: a subset of quantum physics explaining the physical behaviours at atomic and sub-atomic levels*Old quantum theory under the Bohr model...
.
It is possible to consider valid transformations on the states of a group of elementary systems, although the mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of such an analysis is more complicated than the case for a single system. Transformations consisting of a valid transformation on each state acting independently are always valid. In the case of a two system model, there is also a transformation which is analogous to the c-not
Controlled NOT gate
The Controlled NOT gate is a quantum gate that is an essential component in the construction of a quantum computer. It can be used to disentangle EPR states...
operator on qubits. Furthermore, within the bounds of the model it is possible to prove no-cloning and no-broadcasting theorems, reproducing a fair deal of the mechanics of quantum information theory.
The monogamy
Monogamy
Monogamy /Gr. μονός+γάμος - one+marriage/ a form of marriage in which an individual has only one spouse at any one time. In current usage monogamy often refers to having one sexual partner irrespective of marriage or reproduction...
of pure entanglement also has a strong analogue within the toy model, as a group of three or more systems in which knowledge of one system would grant knowledge of the others would break the knowledge balance principle. An analogy of quantum teleportation
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
also exists in the model, as well as a number of important quantum phenomena.
Extensions and further work
Work has been done on several models of physical systems with similar characteristics, which are described in detail in the main paper on this model. There are ongoing attempts to extend this model in various ways, such as van Enk's model and the "Pacman Version".Currently, there is work being done to reproduce quantum formalism
Formalism
The term formalism describes an emphasis on form over content or meaning in the arts, literature, or philosophy. A practitioner of formalism is called a formalist. A formalist, with respect to some discipline, holds that there is no transcendent meaning to that discipline other than the literal...
from information-theoretic axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s. Although the model itself differs in many respects from quantum theory, it reproduces a number of effects which are considered to be overwhelmingly quantum. As such, the underlying principle, that quantum states are states of incomplete knowledge
Knowledge
Knowledge is a familiarity with someone or something unknown, which can include information, facts, descriptions, or skills acquired through experience or education. It can refer to the theoretical or practical understanding of a subject...
, may offer some hints as to how to proceed in this manner, and may lend hope to those pursuing this goal.