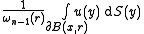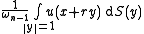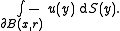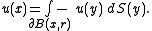In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the spherical mean of a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 around a point is the average of all values of that function on a sphere of given radius centered at that point.

Definition

Consider an open set

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 U in the Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 Rⁿ and a continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

 u defined on U with real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 or complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

 values. Let x be a point in U and r > 0 be such that the closed

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

 ball

Ball (mathematics)

In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....

 B(x, r) of center x and radius r is contained in U. The spherical mean over the sphere of radius r centered at x is defined as

where ∂B(x, r) is the (n−1)-sphere forming the boundary

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

 of B(x, r), dS denotes integration with respect to spherical measure

Spherical measure

In mathematics — specifically, in geometric measure theory — spherical measure σn is the “natural” Borel measure on the n-sphere Sn. Spherical measure is often normalized so that it is a probability measure on the sphere, i.e...

 and ω_n−1(r) is the "surface area" of this (n−1)-sphere.

Equivalently, the spherical mean is given by

where ω_n−1 is the area of the (n−1)-sphere of radius 1.

The spherical mean is often denoted as

Properties and uses

• From the continuity of it follows that the function

is continuous, and its limit

Limit of a function

In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....

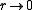 as is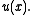

• Spherical means are used in finding the solution of the wave equation
  Wave equation
  The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
  
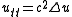    for 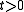with prescribed boundary conditions at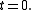

• If 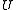is an open set in 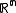and is a C²
  Smooth function
  In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
  
   function defined on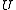 , then is harmonic
  Harmonic function
  In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
  
   if and only if for all in 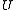and all 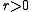such that the closed ball 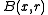is contained in 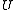one has

This result can be used to prove the maximum principle

Maximum principle

In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...

for harmonic functions.