
Tree automaton
Encyclopedia
A tree automaton is a type of state machine. Tree automata deal with tree structure
s, rather than the strings
of more conventional state machines.
The following article deals with branching tree automata, which correspond to regular languages of trees. For a different notion of tree automaton, see tree walking automaton
.
As with classical automata, finite tree automata (FTA) can be either a deterministic automaton
or not. According to how the automaton processes the input tree, finite tree automata can be of two types: (a) bottom up, (b) top down. This is an important issue, as although non-deterministic (ND) top-down and ND bottom-up tree automata are equivalent in expressive power, deterministic top-down automata are strictly less powerful than their deterministic bottom-up counterparts, because tree properties specified by deterministic top-down tree automata can only depend on path properties. (Deterministic bottom-up tree automata are as powerful as ND tree automata.)
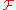 and a function
and a function  . Each letter has its arity
. Each letter has its arity
so it can be used to build terms
. Nullary elements (of zero arity) are also called constants. Terms built with unary symbols and constants can be considered as strings
. Higher arity leads to trees
.
A bottom-up finite tree automaton over is defined by:
is defined by:
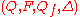
Here is a set of unary letters (states),
is a set of unary letters (states),  is a ranked alphabet,
is a ranked alphabet, 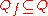 is a set of final states, and
is a set of final states, and  is a set of transition rules
is a set of transition rules
, that is, rewrite rules from nodes whose childs' roots are states, to nodes whose roots are states. Thus the state of a node is deduced from the states of its children.
There is no initial state as such, but the transition rules for constant symbols (leaves) can be considered as initial states. The tree is accepted if the state labeled at the root is an accepting state.
A top-down finite tree automaton over is defined by:
is defined by:

There are two differences with bottom-up tree automata : first, , the set of its initial states, replaces
, the set of its initial states, replaces  ; second, its transition rules are the converse, that is, rewrite rules from nodes whose roots are states to nodes whose child's roots are states. The tree is accepted if every branch can be gone through this way.
; second, its transition rules are the converse, that is, rewrite rules from nodes whose roots are states to nodes whose child's roots are states. The tree is accepted if every branch can be gone through this way.
The rewrite rules cause symbols from to 'travel' along branches of the tree.
to 'travel' along branches of the tree.
One can easily guess that non-deterministic top-down tree automata are equivalent to non-deterministic bottom-up ones ; the transition rules are simply reversed, and the final states become the initial states.
Why then are deterministic top-down FTA less powerful than their bottom-up counterparts? Because a deterministic TA is by definition one where no two transition rules have the same left-hand side. For tree automata, transition rules are rewrite rules ; and for top-down ones, the left-hand side will be parent nodes. Consequently a deterministic top-down tree automaton will only be able to test for tree properties that are true in all branches, because the choice of the state to write into each child branch is determined at the parent node, without knowing the child branches contents.
 (that is, a tree) is accepted if there exists a reduction that starts from t and ends with q(t), where q is a final state. For a top-down automaton, a ground term
(that is, a tree) is accepted if there exists a reduction that starts from t and ends with q(t), where q is a final state. For a top-down automaton, a ground term  is accepted if there exists a reduction that starts from q(t) and ends with t, where q(t) is an initial state.
is accepted if there exists a reduction that starts from q(t) and ends with t, where q(t) is an initial state.
The tree language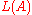 recognized by a tree automaton
recognized by a tree automaton  is the set of all ground terms accepted by
is the set of all ground terms accepted by  . A set of ground terms is recognizable if there exists a tree automaton that recognizes it.
. A set of ground terms is recognizable if there exists a tree automaton that recognizes it.
One important property is that linear (that is, arity-preserving) homomorphisms preserve recognizability.
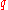 is accessible if there exists a ground term
is accessible if there exists a ground term  such that there exists a reduction from
such that there exists a reduction from  to
to 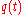 . An FTA is reduced if all its states are accessible.
. An FTA is reduced if all its states are accessible.
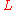 be a recognizable set of ground terms. Then, there exists a constant
be a recognizable set of ground terms. Then, there exists a constant  satisfying: for every ground term
satisfying: for every ground term  in
in 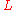 such that
such that 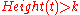 , there exists a context
, there exists a context 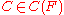 , a non trivial context
, a non trivial context 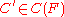 and a ground term
and a ground term  such that
such that  and, for all
and, for all 
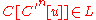 .
.
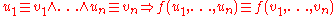
It is of finite index if its number of equivalence-classes is finite.
For a given tree-language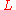 , define
, define  if for all contexts
if for all contexts 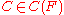 ,
,  .
.
The Myhill-Nerode Theorem for tree automaton states that the following three statements are equivalent:
(OCaml) Timbuk - Tools for Reachability Analysis and Tree Automata Calculations (http://www.irisa.fr/celtique/genet/timbuk/)
(Java) LETHAL - Library for working with finite tree and hedge automata (http://lethal.sf.net/)
(Isabelle [OCaml, SML, Haskell]) - Machine-Checked Tree Automata Library (http://afp.sourceforge.net/entries/Tree-Automata.shtml)
(C++) VATA: A Library for Efficient Manipulation of Non-Deterministic Tree Automata - (http://www.fit.vutbr.cz/research/groups/verifit/tools/libvata/)
Tree structure
A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
s, rather than the strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
of more conventional state machines.
The following article deals with branching tree automata, which correspond to regular languages of trees. For a different notion of tree automaton, see tree walking automaton
Tree walking automaton
A tree walking automaton is a type of finite automaton that deals with tree structures rather than strings. The concept was originally proposed in .The following article deals with tree walking automata...
.
As with classical automata, finite tree automata (FTA) can be either a deterministic automaton
Deterministic automaton
Deterministic automaton is a concept of automata theory in which the outcome of a transition from one state to another given a certain input can be predicted for every occurrence....
or not. According to how the automaton processes the input tree, finite tree automata can be of two types: (a) bottom up, (b) top down. This is an important issue, as although non-deterministic (ND) top-down and ND bottom-up tree automata are equivalent in expressive power, deterministic top-down automata are strictly less powerful than their deterministic bottom-up counterparts, because tree properties specified by deterministic top-down tree automata can only depend on path properties. (Deterministic bottom-up tree automata are as powerful as ND tree automata.)
Definitions
A ranked alphabet is a pair of ordinary alphabet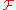 and a function
and a function  . Each letter has its arity
. Each letter has its arityArity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
so it can be used to build terms
Term (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
. Nullary elements (of zero arity) are also called constants. Terms built with unary symbols and constants can be considered as strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
. Higher arity leads to trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
.
A bottom-up finite tree automaton over
 is defined by:
is defined by: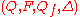
Here
 is a set of unary letters (states),
is a set of unary letters (states),  is a ranked alphabet,
is a ranked alphabet, 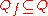 is a set of final states, and
is a set of final states, and  is a set of transition rules
is a set of transition rulesProduction (computer science)
A production or production rule in computer science is a rewrite rule specifying a symbol substitution that can be recursively performed to generate new symbol sequences. A finite set of productions P is the main component in the specification of a formal grammar...
, that is, rewrite rules from nodes whose childs' roots are states, to nodes whose roots are states. Thus the state of a node is deduced from the states of its children.
There is no initial state as such, but the transition rules for constant symbols (leaves) can be considered as initial states. The tree is accepted if the state labeled at the root is an accepting state.
A top-down finite tree automaton over
 is defined by:
is defined by:
There are two differences with bottom-up tree automata : first,
 , the set of its initial states, replaces
, the set of its initial states, replaces  ; second, its transition rules are the converse, that is, rewrite rules from nodes whose roots are states to nodes whose child's roots are states. The tree is accepted if every branch can be gone through this way.
; second, its transition rules are the converse, that is, rewrite rules from nodes whose roots are states to nodes whose child's roots are states. The tree is accepted if every branch can be gone through this way.The rewrite rules cause symbols from
 to 'travel' along branches of the tree.
to 'travel' along branches of the tree.One can easily guess that non-deterministic top-down tree automata are equivalent to non-deterministic bottom-up ones ; the transition rules are simply reversed, and the final states become the initial states.
Why then are deterministic top-down FTA less powerful than their bottom-up counterparts? Because a deterministic TA is by definition one where no two transition rules have the same left-hand side. For tree automata, transition rules are rewrite rules ; and for top-down ones, the left-hand side will be parent nodes. Consequently a deterministic top-down tree automaton will only be able to test for tree properties that are true in all branches, because the choice of the state to write into each child branch is determined at the parent node, without knowing the child branches contents.
Determinism
As said before, a deterministic tree automaton is one where no two transition rules have the same left-hand side. This definition matches the intuitive idea that for an automaton to be deterministic, one and only one transition must be possible for a given node.Recognizability
For a bottom-up automaton, a ground term (that is, a tree) is accepted if there exists a reduction that starts from t and ends with q(t), where q is a final state. For a top-down automaton, a ground term
(that is, a tree) is accepted if there exists a reduction that starts from t and ends with q(t), where q is a final state. For a top-down automaton, a ground term  is accepted if there exists a reduction that starts from q(t) and ends with t, where q(t) is an initial state.
is accepted if there exists a reduction that starts from q(t) and ends with t, where q(t) is an initial state.The tree language
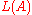 recognized by a tree automaton
recognized by a tree automaton  is the set of all ground terms accepted by
is the set of all ground terms accepted by  . A set of ground terms is recognizable if there exists a tree automaton that recognizes it.
. A set of ground terms is recognizable if there exists a tree automaton that recognizes it.One important property is that linear (that is, arity-preserving) homomorphisms preserve recognizability.
Completeness and Reduction
A non-deterministic finite tree automaton is complete if there is at least one transition rule available for every possible symbol-states combination. A state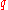 is accessible if there exists a ground term
is accessible if there exists a ground term  such that there exists a reduction from
such that there exists a reduction from  to
to 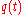 . An FTA is reduced if all its states are accessible.
. An FTA is reduced if all its states are accessible.Pumping Lemma
Let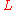 be a recognizable set of ground terms. Then, there exists a constant
be a recognizable set of ground terms. Then, there exists a constant  satisfying: for every ground term
satisfying: for every ground term  in
in 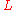 such that
such that  , there exists a context
, there exists a context 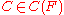 , a non trivial context
, a non trivial context 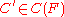 and a ground term
and a ground term  such that
such that  and, for all
and, for all 
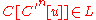 .
.Closure
The class of recognizable tree languages is closed under union, under complementation, and under intersection.Myhill-Nerode Theorem
A congruence on tree languages is a relation such that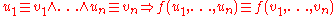
It is of finite index if its number of equivalence-classes is finite.
For a given tree-language
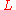 , define
, define  if for all contexts
if for all contexts 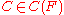 ,
,  .
.The Myhill-Nerode Theorem for tree automaton states that the following three statements are equivalent:
- L is a recognizable tree language
- L is the union of some equivalence classes of congruence of finite index
- the relation
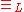 is a congruence of finite index
is a congruence of finite index
External links
All the information in this page was taken from Chapter 1 of http://tata.gforge.inria.frImplementations
(OCaml) Grappa - Ranked and Unranked Tree Automata Libraries (http://www.grappa.univ-lille3.fr/~filiot/tata/)(OCaml) Timbuk - Tools for Reachability Analysis and Tree Automata Calculations (http://www.irisa.fr/celtique/genet/timbuk/)
(Java) LETHAL - Library for working with finite tree and hedge automata (http://lethal.sf.net/)
(Isabelle [OCaml, SML, Haskell]) - Machine-Checked Tree Automata Library (http://afp.sourceforge.net/entries/Tree-Automata.shtml)
(C++) VATA: A Library for Efficient Manipulation of Non-Deterministic Tree Automata - (http://www.fit.vutbr.cz/research/groups/verifit/tools/libvata/)

