1.96 - AbsoluteAstronomy.com

1.96 is the approximate value of the 97.5 percentile

Percentile

In statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...

point of the normal distribution used in probability

Probability

Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...

and statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

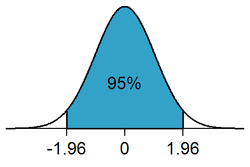
. 95% of the area under a normal curve lies within roughly 1.96 standard deviation

Standard deviation

Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...

s of the mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

, and due to the central limit theorem

Central limit theorem

In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...

, this number is therefore used in the construction of approximate 95% confidence interval

Confidence interval

In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...

s. Its ubiquity is due to the arbitrary but common convention of using confidence intervals with 95% coverage rather than other coverages (such as 90% or 99%). This convention seems particularly common in medical statistics, but is also common in other areas of application, such as earth sciences and business research.

There is no single accepted name for this number; it is also commonly referred to as the "standard normal deviate

Deviation (statistics)

In mathematics and statistics, deviation is a measure of difference for interval and ratio variables between the observed value and the mean. The sign of deviation , reports the direction of that difference...

", "normal score

Normal score

The term normal score is used with two different meanings in statistics. One of them relates to creating a single value which can be treated as if it had arisen from a standard normal distribution...

" or "Z score" for the 97.5 percentile point, or .975 point.

If X has a standard normal distribution, i.e. X ~ N(0,1),

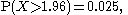
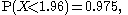
and as the normal distribution is symmetric,

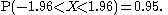
One notation for this number is z_.025.
From the probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

of the normal distribution, the exact value of z_.025 is determined by

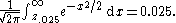
History

The use of this number in applied statistics can be traced to the influence of Ronald Fisher

Ronald Fisher

Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...

's classic textbook, Statistical Methods for Research Workers

Statistical Methods for Research Workers

Statistical Methods for Research Workers is a classic 1925 book on statistics by the statistician R.A. Fisher. It is considered by some to be one of the 20th century's most influential books on statistical methods. According to ,...

, first published in 1925:

"The value for which P = .05, or 1 in 20, is 1.96 or nearly 2 ; it is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not."

In Table 1 of the same work, he gave the more precise value 1.959964.
In 1970, the value truncated to 20 decimal places was calculated to be

1.95996 39845 40054 23552...

The commonly-used approximate value of 1.96 is therefore accurate to better than one part in 50 000, which is more than adequate for applied work.

Software functions

The inverse of the standard normal CDF

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

can be used to compute the value. The following is a table of function calls that return 1.96 in some commonly used applications:

Application	Function call
Excel Microsoft Excel Microsoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...	NORMSINV(0.975)
Mathematica Mathematica Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...	InverseCDF NormalDistribution[0,1],0.975]
MATLAB MATLAB MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...	max(norminv([0.025, 0.975]))
R R (programming language) R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....	qnorm(0.975)

History

Software functions

See also