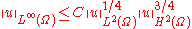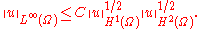Agmon's inequality
Encyclopedia
In mathematical analysis
, Agmon's inequalities, named after Shmuel Agmon
, consist of a few closely related inequalities between the Lebesgue space
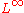 and the Sobolev space
and the Sobolev space
s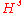 . It is useful in the study of partial differential equation
. It is useful in the study of partial differential equation
s.
The result is stated in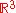 only. Let
only. Let  be a vector-valued function,
be a vector-valued function, 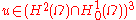 where
where  . Then Agmon's inequalities state that there exists a constant
. Then Agmon's inequalities state that there exists a constant  such that
such that
and
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Agmon's inequalities, named after Shmuel Agmon
Shmuel Agmon
Shmuel Agmon is an Israeli mathematician. He is known for his work in analysis and partial differential equations.-Work:...
, consist of a few closely related inequalities between the Lebesgue space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
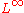 and the Sobolev space
and the Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s
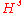 . It is useful in the study of partial differential equation
. It is useful in the study of partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s.
The result is stated in
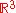 only. Let
only. Let  be a vector-valued function,
be a vector-valued function, 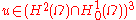 where
where  . Then Agmon's inequalities state that there exists a constant
. Then Agmon's inequalities state that there exists a constant  such that
such thatand