
Allen's Interval Algebra
Encyclopedia
For the type of boolean algebra called interval algebra, see Boolean algebra (structure)
Allen's interval algebra is a calculus for temporal reasoning
that was introduced by James F. Allen
in 1983.
The calculus defines possible relations between time intervals and provides a composition table that can be used as a basis
for reasoning about temporal descriptions of events.
!Relation
!Illustration
!Interpretation
|-
|

|
|X takes place before Y
|-
|
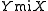
|
|X meets Y (i stands for inverse)
|-
|
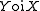
|
|X overlaps with Y
|-
|

|
|X starts Y
|-
|
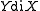
|
|X during Y
|-
|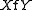
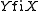
|
|X finishes Y
|-
|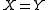
|
|X is equal to Y
|}>
Using this calculus, given facts can be formalized and then used for automatic reasoning. Relations between intervals are formalized as sets of base relations.
The sentence
is formalized in Allen's Interval Algebra as follows:
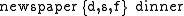
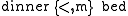
In general, the number of different relations between n intervals is 1, 1, 13, 409, 23917, 2244361... OEIS A055203. The special case shown above is for n=2.
 and
and 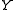 and the relation between
and the relation between  and
and 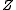 , the composition table allows for concluding about the relation between
, the composition table allows for concluding about the relation between 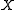 and
and 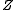 . Together with a converse
. Together with a converse
operation, this turns Allen's Interval Algebra into a relation algebra
.
For the example, one can infer .
.
Allen's interval algebra is a calculus for temporal reasoning
Spatial-temporal reasoning
Spatial–temporal reasoning is used in both the fields of psychology and computer science.-Spatial–temporal reasoning in psychology:Spatial-temporal reasoning is the ability to visualize spatial patterns and mentally manipulate them over a time-ordered sequence of spatial transformations.This...
that was introduced by James F. Allen
James F. Allen
James Frederick Allen is a computational linguist recognized for his contributions to temporal logic, in particular Allen's Interval Algebra. He is the John H. Dessaurer Professor of Computer Science at the University of Rochester.-Biography:...
in 1983.
The calculus defines possible relations between time intervals and provides a composition table that can be used as a basis
for reasoning about temporal descriptions of events.
Relations
The following 13 base relations capture the possible relations between two intervals.!Illustration
!Interpretation
|-
|


|
|X takes place before Y
|-
|

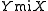
|
|X meets Y (i stands for inverse)
|-
|

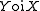
|
|X overlaps with Y
|-
|


|
|X starts Y
|-
|

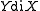
|
|X during Y
|-
|
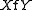
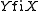
|
|X finishes Y
|-
|
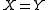
|
|X is equal to Y
|}>
Using this calculus, given facts can be formalized and then used for automatic reasoning. Relations between intervals are formalized as sets of base relations.
The sentence
- During dinner, Peter reads newspaper. Afterwards, he goes to bed.
is formalized in Allen's Interval Algebra as follows:
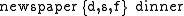
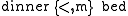
In general, the number of different relations between n intervals is 1, 1, 13, 409, 23917, 2244361... OEIS A055203. The special case shown above is for n=2.
Composition of relations between intervals
For reasoning about the relations between temporal intervals, Allen's Interval Algebra provides a composition table. Given the relation between and
and 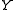 and the relation between
and the relation between  and
and 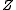 , the composition table allows for concluding about the relation between
, the composition table allows for concluding about the relation between 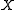 and
and 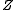 . Together with a converse
. Together with a converseInverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
operation, this turns Allen's Interval Algebra into a relation algebra
Relation algebra
In mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
.
For the example, one can infer
 .
.
