
Anderson's theorem
Encyclopedia
In mathematics
, Anderson's
theorem is a result in real analysis
and geometry
which says that the integral
of an integrable, symmetric, unimodal, non-negative function f over an n-dimensional convex body
K does not decrease if K is translated inwards towards the origin. This is a natural statement, since the graph
of f can be thought of as a hill with a single peak over the origin; however, for n ≥ 2, the proof is not entirely obvious, as there may be points x of the body K where the value f(x) is larger than at the corresponding translate of x.
Anderson's theorem also has an interesting application to probability theory
.
al Euclidean space
Rn that is symmetric
with respect to reflection in the origin, i.e. K = −K. Let f : Rn → R be a non-negative, symmetric, globally integrable function; i.e.
Suppose also that the super-level set
s L(f, t) of f, defined by
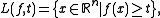
are convex subsets
of Rn for every t ≥ 0. (This property is sometimes referred to as being unimodal.) Then, for any 0 ≤ c ≤ 1 and y ∈ Rn,
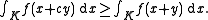
(Ω, Σ, Pr), suppose that X : Ω → Rn is an Rn-valued random variable
with probability density function
f : Rn → [0, +∞) and that Y : Ω → Rn is an independent
random variable. The probability density functions of many well-known probability distributions are p-concave
for some p, and hence unimodal. If they are also symmetric (e.g. the Laplace and normal distributions), then Anderson's theorem applies, in which case

for any origin-symmetric convex body K ⊆ Rn.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Anderson's
Theodore Wilbur Anderson
Theodore Wilbur Anderson is an American mathematician and statistician who has specialized in the analysis of multivariate data.Born in Minneapolis, Minnesota, he was awarded a Guggenheim Fellowship in 1946....
theorem is a result in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
which says that the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of an integrable, symmetric, unimodal, non-negative function f over an n-dimensional convex body
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
K does not decrease if K is translated inwards towards the origin. This is a natural statement, since the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of f can be thought of as a hill with a single peak over the origin; however, for n ≥ 2, the proof is not entirely obvious, as there may be points x of the body K where the value f(x) is larger than at the corresponding translate of x.
Anderson's theorem also has an interesting application to probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
Statement of the theorem
Let K be a convex body in n-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn that is symmetric
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
with respect to reflection in the origin, i.e. K = −K. Let f : Rn → R be a non-negative, symmetric, globally integrable function; i.e.
- f(x) ≥ 0 for all x ∈ Rn;
- f(x) = f(−x) for all x ∈ Rn;
-
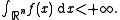
Suppose also that the super-level set
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
s L(f, t) of f, defined by
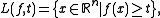
are convex subsets
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
of Rn for every t ≥ 0. (This property is sometimes referred to as being unimodal.) Then, for any 0 ≤ c ≤ 1 and y ∈ Rn,
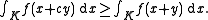
Application to probability theory
Given a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, Σ, Pr), suppose that X : Ω → Rn is an Rn-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
f : Rn → [0, +∞) and that Y : Ω → Rn is an independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variable. The probability density functions of many well-known probability distributions are p-concave
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
for some p, and hence unimodal. If they are also symmetric (e.g. the Laplace and normal distributions), then Anderson's theorem applies, in which case

for any origin-symmetric convex body K ⊆ Rn.

