In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, Apollonius' theorem is a theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

 relating the length of a median

Median (geometry)

In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...

 of a triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

 to the lengths of its side.
Specifically, in any triangle ABC, if AD is a median, then
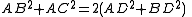
It is a special case of Stewart's theorem

Stewart's theorem

In geometry, Stewart's theorem yields a relation between a lengths of the sides of the triangle and the length of a cevian of the triangle. Its name is in honor of the Scottish mathematician Matthew Stewart who published the theorem in 1746.- Theorem :...

. For an isosceles triangle the theorem reduces to the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

. From the fact that diagonals of a parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

 bisect each other, the theorem is equivalent to the parallelogram law

Parallelogram law

In mathematics, the simplest form of the parallelogram law belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals...

.

The theorem is named for Apollonius of Perga

Apollonius of Perga

Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...

.

Proof

The theorem can be proved as a special case of Stewart's theorem

Stewart's theorem

In geometry, Stewart's theorem yields a relation between a lengths of the sides of the triangle and the length of a cevian of the triangle. Its name is in honor of the Scottish mathematician Matthew Stewart who published the theorem in 1746.- Theorem :...

, or can be proved using vectors (see parallelogram law

Parallelogram law

In mathematics, the simplest form of the parallelogram law belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals...

). The following is an independent proof using the law of cosines

Law of cosines

In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...

.

Let the triangle have sides a, b, c with a median d drawn to side a. Let m be the length of the segments of a formed by the median, so m is half of a. Let the angles formed between a and d be θ and θ′ where θ includes b and θ′ includes c. Then θ′ is the supplement of θ and cos θ′ = −cos θ. The law of cosines

Law of cosines

In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...

for θ and θ′ states

Add these equations to obtain
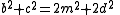
as required.