Banach's matchbox problem
Encyclopedia
Banach's match problem is a classic problem in probability
attributed to Stefan Banach
. Feller says that the problem was inspired by a humorous reference to Banach's smoking habit in a speech honouring him by H. Steinhaus, but that it was not Banach who set the problem or provided an answer.
Suppose a mathematician carries two matchboxes at all times: one in his left pocket and one in his right. Each time he needs a match, he is equally likely to take it from either pocket. Suppose he reaches into his pocket and discovers that the box picked is empty. If it is assumed that each of the matchboxes originally contained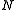
matches, what is the probability that there are exactly 
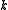matches in the other box?
and thus
.
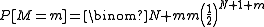Returning to the original problem, we see that the probability that the left pocket is found to be empty first is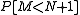
which equals 1/2 because both are equally likely. We see that the number K of matches remaining in the other pocket is
.
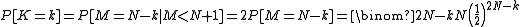Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
attributed to Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
. Feller says that the problem was inspired by a humorous reference to Banach's smoking habit in a speech honouring him by H. Steinhaus, but that it was not Banach who set the problem or provided an answer.
Suppose a mathematician carries two matchboxes at all times: one in his left pocket and one in his right. Each time he needs a match, he is equally likely to take it from either pocket. Suppose he reaches into his pocket and discovers that the box picked is empty. If it is assumed that each of the matchboxes originally contained
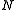matches, what is the probability that there are exactly 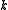matches in the other box?Solution
First consider the case where the matchbox in his right pocket has an unlimited number of matches and let M be the number of matches removed from this one before the left one is found to be empty. When the left pocket is found to be empty, the man has chosen that pocket (N+1) times. Then M is the number of successes before (N+1) failures in Bernoulli trials with p=1/2, which has the negative binomial distributionNegative binomial distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
and thus
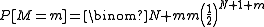.Returning to the original problem, we see that the probability that the left pocket is found to be empty first is
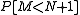which equals 1/2 because both are equally likely. We see that the number K of matches remaining in the other pocket is.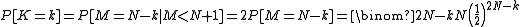