In real analysis

Real analysis

Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...

, Bernoulli's inequality (named after Jacob Bernoulli) is an inequality that approximates exponentiation

Exponentiation

Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...

s of 1 + x.

The inequality states that


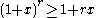
for every integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

 r ≥ 0 and every real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 x ≥ −1. If the exponent r is even, then the inequality is valid for all real numbers x. The strict version of the inequality reads


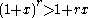
for every integer r ≥ 2 and every real number x ≥ −1 with x ≠ 0.

Bernoulli's inequality is often used as the crucial step in the proof of other inequalities. It can itself be proved using mathematical induction

Mathematical induction

Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...

, as shown below.

Proof of the inequality

For r = 0,


is equivalent to 1 ≥ 1 which is true as required.

Now suppose the statement is true for r = k:


Then it follows that


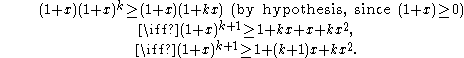
However, as 1 + (k + 1)x + kx² ≥ 1 + (k + 1)x (since kx² ≥ 0), it follows that (1 + x)^k + 1 ≥ 1 + (k + 1)x, which means the statement is true for r = k + 1 as required.

By induction we conclude the statement is true for all r ≥ 0.

Generalization

The exponent r can be generalized to an arbitrary real number as follows: if x > −1, then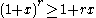


for r ≤ 0 or r ≥ 1, and


for 0 ≤ r ≤ 1.

This generalization can be proved by comparing derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

s.
Again, the strict versions of these inequalities require x ≠ 0 and r ≠ 0, 1.

Related inequalities

The following inequality estimates the r-th power of 1 + x from the other side. For any real numbers x, r > 0, one has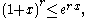


where e = 2.718.... This may be proved using the inequality (1 + 1/k)^k < e.

External links

• Bernoulli Inequality by Chris Boucher, Wolfram Demonstrations Project
  Wolfram Demonstrations Project
  The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
  
  .