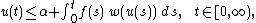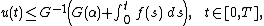Bihari's inequality
Encyclopedia
Bihari's inequality, proved by Hungarian mathematician Imre Bihari (1915–1998), is the following nonlinear generalization of the Grönwall's lemma.
Let u and ƒ be non-negative continuous functions defined on [0, ∞), and let w be a continuous non-decreasing function defined on [0, ∞) and w(u) > 0 on (0, ∞). If u satisfies the following integral inequality,
where α is a non-negative constant, then
where the function G is defined by
and G−1 is the inverse function of G and T is chosen so that
Let u and ƒ be non-negative continuous functions defined on [0, ∞), and let w be a continuous non-decreasing function defined on [0, ∞) and w(u) > 0 on (0, ∞). If u satisfies the following integral inequality,
where α is a non-negative constant, then
where the function G is defined by
and G−1 is the inverse function of G and T is chosen so that