
Birch's theorem
Encyclopedia
In mathematics, Birch's theorem, named for Bryan John Birch
, is a statement about the representability of zero by odd degree forms.
, k, l and n be natural numbers, r1,...,rk be odd natural numbers, and f1,...,fk be homogeneous polynomials with coefficients in K of degrees r1,...,rk respectively in n variables, then there exists a number ψ(r1,...,rk,l,K) such that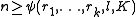
implies that there exists an l-dimensional vector subspace V of Kn such that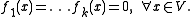
over the maximal degree of the forms f1,...,fk. Essential to the proof is a special case, which can be proved by an application of the Hardy-Littlewood circle method
, of the theorem which states that if n is sufficiently large and r is odd, then the equation
has a solution in integers x1,...,xn, not all of which are 0.
The restriction to odd r is necessary, since even-degree forms, such as positive definite quadratic forms, may take the value 0 only at the origin.
Bryan John Birch
Bryan John Birch F.R.S. is a British mathematician. His name has been given to the Birch and Swinnerton-Dyer conjecture....
, is a statement about the representability of zero by odd degree forms.
Statement of Birch's theorem
Let K be an algebraic number fieldAlgebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
, k, l and n be natural numbers, r1,...,rk be odd natural numbers, and f1,...,fk be homogeneous polynomials with coefficients in K of degrees r1,...,rk respectively in n variables, then there exists a number ψ(r1,...,rk,l,K) such that
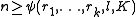
implies that there exists an l-dimensional vector subspace V of Kn such that
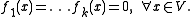
Remarks
The proof of the theorem is by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
over the maximal degree of the forms f1,...,fk. Essential to the proof is a special case, which can be proved by an application of the Hardy-Littlewood circle method
Hardy-Littlewood circle method
In mathematics, the Hardy–Littlewood circle method is one of the most frequently used techniques of analytic number theory. It is named for G. H. Hardy and J. E...
, of the theorem which states that if n is sufficiently large and r is odd, then the equation

has a solution in integers x1,...,xn, not all of which are 0.
The restriction to odd r is necessary, since even-degree forms, such as positive definite quadratic forms, may take the value 0 only at the origin.

