Bochner's theorem
Encyclopedia
In mathematics
, Bochner's theorem (named for Salomon Bochner
) characterizes the Fourier transform of a positive finite Borel measure on the real line.
Q of μ is the continuous function
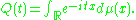
Q is continuous since for a fixed x, the function e-itx is continuous and periodic. The function Q is a positive definite function, i.e. the kernel K(x, y) = Q(y - x) is positive definite; this can be checked via a direct calculation.
Let F0(R) be the family of complex valued functions on R with finite support, i.e. f(x) = 0 for all but finitely many x. The positive definite kernel K(x, y) induces a sesquilinear form
on F0(R). This in turn results in a Hilbert space
whose typical element is an equivalence class [g]. For a fixed t in R, the "shift operator
" Ut defined by (Utg)(x) = g(x - t), for a representative of [g] is unitary. In fact the map
is a strongly continuous representation
of the additive group R. By the Stone-von Neumann theorem, there exists a (possibly unbounded) self-adjoint operator
A such that
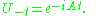
This implies there exists a finite positive Borel measure μ on R where
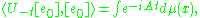
where e0 is the element in F0(R) defined by e0(m) = 1 if m = 0 and 0 otherwise. Because
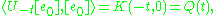
the theorem holds.
, one often has to specify a covariance matrix
, the rows and columns of which correspond to observations of some phenomenon. The observations are made at points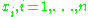
in some space. This matrix is to be a function of the positions of the observations and one usually insists that points which are close to one another have high covariance. One usually specifies that the covariance matrix 
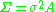where 
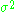is a scalar and matrix 
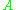is n by n with ones down the main diagonal. Element 
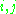of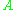 
(corresponding to the correlation between observation i and observation j) is then required to be 
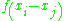for some function 
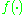, and because 
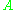must be positive definite, 
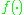must be a positive definite function. Bochner's theorem shows that 
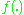must be the characteristic function of a symmetric PDF.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Bochner's theorem (named for Salomon Bochner
Salomon Bochner
Salomon Bochner was an American mathematician of Austrian-Hungarian origin, known for wide-ranging work in mathematical analysis, probability theory and differential geometry.- Life :...
) characterizes the Fourier transform of a positive finite Borel measure on the real line.
Background
Given a positive finite Borel measure μ on the real line R, the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
Q of μ is the continuous function
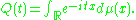
Q is continuous since for a fixed x, the function e-itx is continuous and periodic. The function Q is a positive definite function, i.e. the kernel K(x, y) = Q(y - x) is positive definite; this can be checked via a direct calculation.
The theorem
Bochner's theorem says the converse is true, i.e. every positive definite function Q is the Fourier transform of a positive finite Borel measure. A proof can be sketched as follows.Let F0(R) be the family of complex valued functions on R with finite support, i.e. f(x) = 0 for all but finitely many x. The positive definite kernel K(x, y) induces a sesquilinear form
Sesquilinear form
In mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
on F0(R). This in turn results in a Hilbert space
whose typical element is an equivalence class [g]. For a fixed t in R, the "shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
" Ut defined by (Utg)(x) = g(x - t), for a representative of [g] is unitary. In fact the map
is a strongly continuous representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the additive group R. By the Stone-von Neumann theorem, there exists a (possibly unbounded) self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
A such that
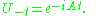
This implies there exists a finite positive Borel measure μ on R where
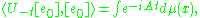
where e0 is the element in F0(R) defined by e0(m) = 1 if m = 0 and 0 otherwise. Because
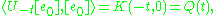
the theorem holds.
Applications
In statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, one often has to specify a covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
, the rows and columns of which correspond to observations of some phenomenon. The observations are made at points
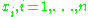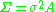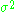in some space. This matrix is to be a function of the positions of the observations and one usually insists that points which are close to one another have high covariance. One usually specifies that the covariance matrix where is a scalar and matrix 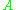is n by n with ones down the main diagonal. Element 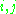of 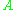(corresponding to the correlation between observation i and observation j) is then required to be 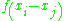for some function 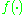, and because 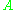must be positive definite, 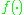must be a positive definite function. Bochner's theorem shows that 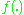must be the characteristic function of a symmetric PDF.