Boltzmann's entropy formula
Encyclopedia
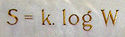
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
S of an ideal gas to the quantity W, which is the number of microstates
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
corresponding to a given macrostate:
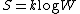(1)where k is Boltzmann's constant equal to 1.38062 x 10−23 joule/kelvin and W is the number of microstate
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
s consistent with the given macrostate.
"Log" is the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
,so the formula can also be notated as:
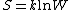
In short, the Boltzmann formula shows the relationship between entropy and the number of ways the atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s or molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s of a thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
can be arranged. In 1934, Swiss physical chemist Werner Kuhn
Werner Kuhn
Werner Kuhn is a Swiss physical chemist who developed the first model of the viscosity of polymer solutions using statistical mechanics. He is known for being the first to apply Boltzmann's entropy formula:S = k \log W \!...
successfully derived a thermal equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
for rubber molecules using Boltzmann's formula, which has since come to be known as the entropy model of rubber.
History
The equation was originally formulated by Ludwig BoltzmannLudwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
between 1872 to 1875, but later put into its current form by Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
in about 1900. To quote Planck, "the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic connection between entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
and probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
was first stated by L. Boltzmann in his kinetic theory
Kinetic theory
The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
of gases."
The value of
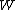was originally intended to be proportional to the Wahrscheinlichkeit (the German word for probability) of a macroscopicMacroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
state for some probability distribution of possible microstates
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
— the collection of (unobservable) "ways" the (observable) thermodynamic
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
state of a system can be realized by assigning different positions
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
and momenta
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
to the various molecules. Interpreted in this way, Boltzmann's formula is the most general formula for the thermodynamic entropy. However, Boltzmann’s paradigm was an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
of
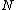identical particles, of which 
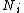are in the 
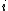-th microscopic condition (range) of position and momentum. For this case, the probability of each microstate of the system is equal, so it was equivalent for Boltzmann to calculate the number of microstates associated with a macrostate. 
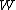was historically misinterpreted as literally meaning the number of microstates, and that is what it usually means today. 
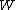can be counted using the formula for permutations
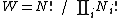(2)where i ranges over all possible molecular conditions and
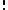denotes factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
. The "correction" in the denominator is due to the fact that identical particles in the same condition are indistinguishable
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
.
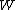is sometimes called the "thermodynamic probability" since it is an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
greater than one, while mathematical probabilities
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
are always number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s between zero and one.
Generalization
Boltzmann's formula applies to microstates of the universe as a whole, each possible microstate of which is presumed to be equally probable.But in thermodynamics it is important to be able to make the approximation of dividing the universe into a system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
of interest, plus its surroundings; and then to be able to identify the entropy of the system with the system entropy in classical thermodynamics. The microstates of such a thermodynamic system are not equally probable—for example, high energy microstates are less probable than low energy microstates for a thermodynamic system kept at a fixed temperature by allowing contact with a heat bath.
For thermodynamic systems where microstates of the system may not have equal probabilities, the appropriate generalization, called the Gibbs entropy, is:
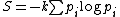(3)This reduces to equation (1) if the probabilities pi are all equal.
Boltzmann used a
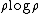formula as early as 1866. He interpreted 
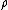as a density in phase space—without mentioning probability—but since this satisfies the axiomatic definition of a probability measure we can retrospectively interpret it as a probability anyway. Gibbs gave an explicitly probabilistic interpretation in 1878.Boltzmann himself used an expression equivalent to (3) in his later work and recognized it as more general than equation (1). That is, equation (1) is a corollary of
equation (3)—and not vice versa. In every situation where equation (1) is valid,
equation (3) is valid also—and not vice versa.
Boltzmann entropy excludes statistical dependencies
The term Boltzmann entropyBoltzmann entropy
In thermodynamics, specifically in statistical mechanics, the Boltzmann entropy is an approximation to the normal Gibbs entropy.The Boltzmann entropy is obtained if one assumes one can treat all the component particles of a thermodynamic system as statistically independent...
is also sometimes used to indicate entropies calculated based on the approximation that the overall probability can be factored into an identical separate term for each particle—i.e., assuming each particle has an identical independent probability distribution, and ignoring interactions and correlations between the particles. This is exact for an ideal gas of identical particles, and may or may not be a good approximation for other systems.