
Bondy's theorem
Encyclopedia
In mathematics, Bondy's theorem is a theorem
in combinatorics
that appeared in a 1972 article by John Adrian Bondy
. The theorem is as follows:
In other words, if we have a 0-1 matrix
with n rows and n columns such that each row is distinct, we can remove one column such that the rows of the resulting n × (n − 1) matrix are distinct.
From the perspective of computational learning theory
, this can be rephrased as follows:
This implies that every finite concept class C has its teaching dimension bounded by |C| − 1.
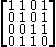
where all rows are pairwise distinct. If we delete, for example, the first column, the resulting matrix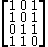
no longer has this property: the first row is identical to the second row. Nevertheless, by Bondy's theorem we know that we can always find a column that can be deleted without introducing any identical rows. In this case, we can delete the third column: all rows of the 3 × 4 matrix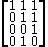
are distinct. Another possibility would have been deleting the fourth column.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
that appeared in a 1972 article by John Adrian Bondy
John Adrian Bondy
John Adrian Bondy, a dual British and Canadian citizen, was a professor of graph theory at the University of Waterloo, in Canada. He is a faculty member of Université Lyon 1, France. Bondy is known for his work on Bondy–Chvátal theorem together with Václav Chvátal. His coauthors include Paul...
. The theorem is as follows:
- Let X be a set with n elements and let A1, A2, ..., An be distinct subsets of X. Then there exists a subset S of X with n − 1 elements such that the sets Ai ∩ S are all distinct.
In other words, if we have a 0-1 matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with n rows and n columns such that each row is distinct, we can remove one column such that the rows of the resulting n × (n − 1) matrix are distinct.
From the perspective of computational learning theory
Computational learning theory
In theoretical computer science, computational learning theory is a mathematical field related to the analysis of machine learning algorithms.-Overview:Theoretical results in machine learning mainly deal with a type of...
, this can be rephrased as follows:
- Let C be a concept classConcept classA concept over a domain X is a total Boolean function over X. A concept class is a class of concepts. Concept class is a subject of computational learning theory....
over a finite domain X. Then there exists a subset S of X with the size at most |C| − 1 such that S is a witness setWitness setIn computational learning theory, let C be a concept class over a domain X and c be a concept in C. A subset S of X is a witness set for c in C if c verifies c...
for every concept in C.
This implies that every finite concept class C has its teaching dimension bounded by |C| − 1.
Example
Consider the 4 × 4 matrix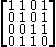
where all rows are pairwise distinct. If we delete, for example, the first column, the resulting matrix

no longer has this property: the first row is identical to the second row. Nevertheless, by Bondy's theorem we know that we can always find a column that can be deleted without introducing any identical rows. In this case, we can delete the third column: all rows of the 3 × 4 matrix

are distinct. Another possibility would have been deleting the fourth column.

