Borel's lemma
Encyclopedia
In mathematics
, Borel's lemma is an important result about partial differential equation
s named after Émile Borel
.
Suppose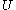
is an open set
in the Euclidean space
Rn, and suppose that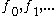
is a sequence
of smooth
, complex
-valued functions
on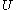
. Then there exists a smooth function 
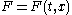defined on R×
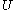with complex values, such that
for all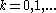
, and 
in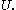 
A constructive proof
of this result is given in Golubitsky and Guillemin (1974).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Borel's lemma is an important result about partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s named after Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
.
Suppose
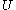is an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, and suppose that
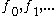is a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on
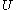. Then there exists a smooth function 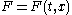defined on R× 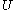with complex values, such thatfor all
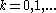, and in 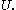A constructive proof
Constructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
of this result is given in Golubitsky and Guillemin (1974).