Brauer's theorem
Encyclopedia
In mathematics
, Brauer's theorem, named for Richard Brauer
, is a result on the representability of 0 by forms over certain fields
in sufficiently many variables.
has a non-trivial (i.e. not all xi are equal to 0) solution in K.
Then, given homogeneous polynomials f1,...,fk of degrees r1,...,rk respectively with coefficients in K, for every set of positive integers r1,...,rk and every non-negative integer l, there exists a number ω(r1,...,rk,l) such that for n ≥ ω(r1,...,rk,l) there exists an l-dimensional affine subspace M of Kn (regarded as a vector space over K) satisfying
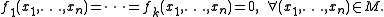
s in the theorem, the equation (*) is satisfied, since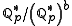
, b a natural number, is finite. Choosing k = 1, one obtains the following corollary:
One can show that if n is sufficiently large according to the above corollary, then n is greater than r2. Indeed, Emil Artin
conjectured that every homogeneous polynomial of degree r over Qp in more than r2 variables represents 0. This is obviously true for r = 1, and it is well-known that the conjecture is true for r = 2 (see, for example, J.-P. Serre, A Course in Arithmetic, Chapter IV, Theorem 6). See quasi-algebraic closure for further context.
In 1950 Demyanov verified the conjecture for r = 3 and p ≠ 3, and in 1952 D. J. Lewis independently proved the case r = 3 for all primes p. But in 1966 Guy Terjanian
constructed a homogeneous polynomial of degree 4 over Q2 in 18 variables that has no non-trivial zero. On the other hand, the Ax–Kochen theorem
shows that for any fixed degree Artin's conjecture is true for all but finitely many Qp.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Brauer's theorem, named for Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
, is a result on the representability of 0 by forms over certain fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
in sufficiently many variables.
Statement of Brauer's theorem
Let K be a field such that for every integer r > 0 there exists an integer ψ(r) such that for n ≥ ψ(r) every equationhas a non-trivial (i.e. not all xi are equal to 0) solution in K.
Then, given homogeneous polynomials f1,...,fk of degrees r1,...,rk respectively with coefficients in K, for every set of positive integers r1,...,rk and every non-negative integer l, there exists a number ω(r1,...,rk,l) such that for n ≥ ω(r1,...,rk,l) there exists an l-dimensional affine subspace M of Kn (regarded as a vector space over K) satisfying
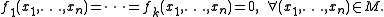
An application to the field of p-adic numbers
Letting K be the field of p-adic numberP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s in the theorem, the equation (*) is satisfied, since
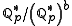, b a natural number, is finite. Choosing k = 1, one obtains the following corollary:- A homogeneous equation f(x1,...,xn) = 0 of degree r in the field of p-adic numbers has a non-trivial solution if n is sufficiently large.
One can show that if n is sufficiently large according to the above corollary, then n is greater than r2. Indeed, Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
conjectured that every homogeneous polynomial of degree r over Qp in more than r2 variables represents 0. This is obviously true for r = 1, and it is well-known that the conjecture is true for r = 2 (see, for example, J.-P. Serre, A Course in Arithmetic, Chapter IV, Theorem 6). See quasi-algebraic closure for further context.
In 1950 Demyanov verified the conjecture for r = 3 and p ≠ 3, and in 1952 D. J. Lewis independently proved the case r = 3 for all primes p. But in 1966 Guy Terjanian
Guy Terjanian
Guy Terjanian is a French-Armenian mathematician who has worked on algebraic number theory. He achieved his Ph.D under Claude Chevalley in 1966, and at that time published a counterexample to the original form of a conjecture of Emil Artin, which suitably modified had just been proved as the...
constructed a homogeneous polynomial of degree 4 over Q2 in 18 variables that has no non-trivial zero. On the other hand, the Ax–Kochen theorem
Ax–Kochen theorem
The Ax–Kochen theorem, named for James Ax and Simon B. Kochen, states that for each positive integer d there is a finite set Yd of prime numbers, such that if p is any prime not in Yd then every homogeneous polynomial of degree d over the p-adic numbers in at least d2+1 variables has a nontrivial...
shows that for any fixed degree Artin's conjecture is true for all but finitely many Qp.