Brauer's three main theorems
Encyclopedia
Brauer's main theorems are three theorems in representation theory of finite groups
linking the blocks
of a finite group
(in characteristic p) with those of its p-local subgroups, that is to say, the normalizers of its non-trivial p-subgroups.
The second and third main theorems allow refinements of orthogonality relations for ordinary character
s which may be applied in finite group theory
. These do not presently admit a proof purely in terms of ordinary characters.
All three main theorems are stated in terms of the Brauer correspondence.
by Brauer. Let G be a finite group, p be a prime, F be a field of characteristic p.
Let H be a subgroup of G which contains
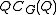
for some p-subgroup Q
of G, and is contained in the normalizer
.
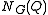The Brauer homomorphism (with respect to H) is a linear map from the center of the group algebra of G over F to the corresponding algebra for H. Specifically, it is the restriction to
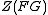of the (linear) projection from 
to 
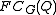whose
kernel is spanned by the elements of G outside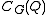
. The image of this map is contained in
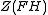, and it transpires that the map is also a ring homomorphism.
Since it is a ring homomorphism
, for any block B of FG, the Brauer homomorphism
sends the identity element of B either to 0 or to an idempotent element. In the latter case,
the idempotent may be decomposed as a sum of (mutually orthogonal) primitive idempotents of Z(FH).
Each of these primitive idempotents is the multiplicative identity of some block of FH. The block b of FH is said to be a Brauer correspondent of B if its identity element occurs
in this decomposition of the image of the identity of B under the Brauer homomorphism.
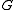is a finite group a 
is a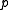 
-subgroup of 
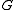, then there is a bijection
between the collections of
(characteristic p) blocks of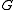
with defect group 
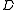and blocks of the normalizer 
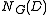with
defect group D. This bijection arises because when
, each block of G
with defect group D has a unique Brauer correspondent block of H, which also has defect
group D.
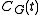to correspond to a given block of 
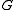, via generalized decomposition numbers. These are the coefficients which occur when the restrictions of ordinary characters of 
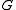(from the given block) to elements of the form tu, where u ranges over elements of order prime to p in 
, are written as linear combinations of the irreducible Brauer character
s of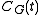
. The content of the theorem is that it is only necessary to use Brauer characters from blocks of 
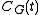which are Brauer correspondents of the chosen block of G.
and H is a subgroup of G, containing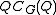
, and contained in 
,
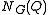then the principal block
of H is the only Brauer correspondent of the principal block of G (where the blocks referred to are calculated in characteristic p).
Representation theory of finite groups
In mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
linking the blocks
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
(in characteristic p) with those of its p-local subgroups, that is to say, the normalizers of its non-trivial p-subgroups.
The second and third main theorems allow refinements of orthogonality relations for ordinary character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
s which may be applied in finite group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. These do not presently admit a proof purely in terms of ordinary characters.
All three main theorems are stated in terms of the Brauer correspondence.
Brauer correspondence
There are many ways to extend the definition which follows, but this is close to the early treatmentsby Brauer. Let G be a finite group, p be a prime, F be a field of characteristic p.
Let H be a subgroup of G which contains
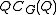
for some p-subgroup Q
of G, and is contained in the normalizer
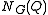.The Brauer homomorphism (with respect to H) is a linear map from the center of the group algebra of G over F to the corresponding algebra for H. Specifically, it is the restriction to
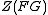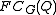of the (linear) projection from to whosekernel is spanned by the elements of G outside
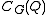. The image of this map is contained in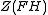, and it transpires that the map is also a ring homomorphism.Since it is a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
, for any block B of FG, the Brauer homomorphism
sends the identity element of B either to 0 or to an idempotent element. In the latter case,
the idempotent may be decomposed as a sum of (mutually orthogonal) primitive idempotents of Z(FH).
Each of these primitive idempotents is the multiplicative identity of some block of FH. The block b of FH is said to be a Brauer correspondent of B if its identity element occurs
in this decomposition of the image of the identity of B under the Brauer homomorphism.
Brauer's first main theorem
Brauer's first main theorem states that if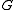 is a finite group a is a 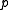-subgroup of 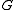, then there is a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the collections of
(characteristic p) blocks of
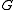with defect group 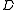and blocks of the normalizer 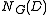withdefect group D. This bijection arises because when
, each block of Gwith defect group D has a unique Brauer correspondent block of H, which also has defect
group D.
Brauer's second main theorem
Brauer's second main theorem gives, for an element t whose order is a power of a prime p, a criterion for a (characteristic p) block of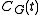 to correspond to a given block of 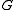, via generalized decomposition numbers. These are the coefficients which occur when the restrictions of ordinary characters of 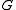(from the given block) to elements of the form tu, where u ranges over elements of order prime to p in , are written as linear combinations of the irreducible Brauer characterModular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
s of
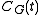. The content of the theorem is that it is only necessary to use Brauer characters from blocks of 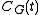which are Brauer correspondents of the chosen block of G.Brauer's third main theorem
Brauer's third main theorem states that when Q is a p-subgroup of the finite group G,and H is a subgroup of G, containing
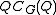, and contained in 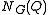,then the principal block
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
of H is the only Brauer correspondent of the principal block of G (where the blocks referred to are calculated in characteristic p).