
Brocard's conjecture
Encyclopedia
In number theory
, Brocard's conjecture is a conjecture
that there are at least four prime number
s between (pn)2 and (pn+1)2, for n > 1, where pn is the nth prime number. It is widely believed that this conjecture is true. However, it remains unproven .
The number of primes between prime squares is 2, 5, 6, 15, 9, 22, 11, 27, ... .
Legendre's conjecture
that there is a prime between consecutive integer squares directly implies that there are at least two primes between prime squares for pn ≥ 3 since pn+1 - pn ≥ 2.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Brocard's conjecture is a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
that there are at least four prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s between (pn)2 and (pn+1)2, for n > 1, where pn is the nth prime number. It is widely believed that this conjecture is true. However, it remains unproven .
| n | 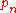 | 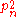 | Prime numbers |  |
|---|---|---|---|---|
| 1 | 2 | 4 | 5, 7 | 2 |
| 2 | 3 | 9 | 11, 13, 17, 19, 23 | 5 |
| 3 | 5 | 25 | 29, 31, 37, 41, 43, 47 | 6 |
| 4 | 7 | 49 | 53, 59, 61, 67, 71… | 15 |
| 5 | 11 | 121 | 127, 131, 137, 139, 149… | 9 |
 stands for stands for 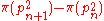 . . |
||||
The number of primes between prime squares is 2, 5, 6, 15, 9, 22, 11, 27, ... .
Legendre's conjecture
Legendre's conjecture
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and 2 for every positive integer n. The conjecture is one of Landau's problems and unproven ....
that there is a prime between consecutive integer squares directly implies that there are at least two primes between prime squares for pn ≥ 3 since pn+1 - pn ≥ 2.

