
Burgers' equation
Encyclopedia
Burgers' equation is a fundamental partial differential equation
from fluid mechanics
. It occurs in various areas of applied mathematics
, such as modeling of gas dynamics
and traffic flow
. It is named for Johannes Martinus Burgers
(1895–1981).
For a given velocity
u and viscosity
coefficient , the general form of Burgers' equation is:
, the general form of Burgers' equation is:
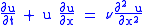 .
.
When , Burgers' equation becomes the inviscid Burgers' equation:
, Burgers' equation becomes the inviscid Burgers' equation:
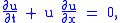
which is a prototype for equations for which the solution can develop discontinuities (shock wave
s). The previous equation is the 'advection form' of the Burgers' equation. The 'conservation form' is:
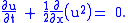
. This method yields that if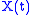 is a solution of the ordinary differential equation
is a solution of the ordinary differential equation
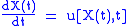
then is constant as a function of
is constant as a function of  . Hence
. Hence  is a solution of the system of ordinary equations:
is a solution of the system of ordinary equations:


The solutions of this system are given in terms of the initial values by:
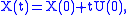

Substitute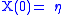 , then
, then 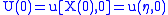 . Now the system becomes
. Now the system becomes


Conclusion:
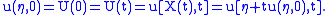
This is an implicit relation that determines the solution of the inviscid Burgers' equation provided characteristics don't intersect. If the characteristics do intersect, then a classical solution to the PDE does not exist.

which turns it into the diffusion equation

That allows one to solve an initial value problem:
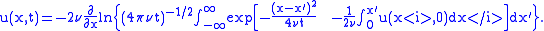

where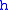 is the debris flow height,
is the debris flow height,  is the time,
is the time,  is the downstream channel position,
is the downstream channel position,  is the pressure gradient and the depth dependent nonlinear variable
is the pressure gradient and the depth dependent nonlinear variable
wave speed, and is a flow height and pressure gradient dependent variable diffusion term.
is a flow height and pressure gradient dependent variable diffusion term.
This equation can also be written in the conservative form:
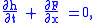
where is the generalized flux that depends on several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient. For
is the generalized flux that depends on several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient. For 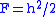 , this equation reduces to the Burgers' equation.
, this equation reduces to the Burgers' equation.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
from fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
. It occurs in various areas of applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, such as modeling of gas dynamics
Gas dynamics
Gas dynamics is a branch of fluid dynamics concerned with studying the motion of gases and its consequent effects. Gas dynamics combines the principles of fluid mechanics and thermodynamics...
and traffic flow
Traffic flow
Traffic flow, in mathematics and civil engineering, is the study of interactions between vehicles, drivers, and infrastructure , with the aim of understanding and developing an optimal road network with efficient movement of traffic and minimal traffic congestion problems.-History:Attempts to...
. It is named for Johannes Martinus Burgers
Johannes Martinus Burgers
-External links:* A.J.Q. Alkemade, , in Biografisch Woordenboek van Nederland. * , biography at the University of Maryland* * at the University of Maryland*...
(1895–1981).
For a given velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
u and viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
coefficient
 , the general form of Burgers' equation is:
, the general form of Burgers' equation is: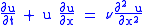 .
.When
 , Burgers' equation becomes the inviscid Burgers' equation:
, Burgers' equation becomes the inviscid Burgers' equation: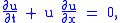
which is a prototype for equations for which the solution can develop discontinuities (shock wave
Shock wave
A shock wave is a type of propagating disturbance. Like an ordinary wave, it carries energy and can propagate through a medium or in some cases in the absence of a material medium, through a field such as the electromagnetic field...
s). The previous equation is the 'advection form' of the Burgers' equation. The 'conservation form' is:
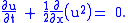
Inviscid Burgers' equation
The inviscid Burgers' equation is a first order partial differential equation (PDE). Its solution can be constructed by the method of characteristicsMethod of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
. This method yields that if
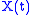 is a solution of the ordinary differential equation
is a solution of the ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
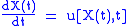
then
 is constant as a function of
is constant as a function of  . Hence
. Hence  is a solution of the system of ordinary equations:
is a solution of the system of ordinary equations:

The solutions of this system are given in terms of the initial values by:
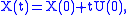

Substitute
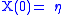 , then
, then 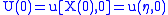 . Now the system becomes
. Now the system becomes

Conclusion:
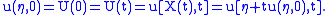
This is an implicit relation that determines the solution of the inviscid Burgers' equation provided characteristics don't intersect. If the characteristics do intersect, then a classical solution to the PDE does not exist.
Viscous Burgers' equation
The viscous Burgers' equation can be linearized by the Cole–Hopf transformation
which turns it into the diffusion equation

That allows one to solve an initial value problem:
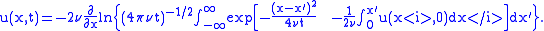
Generalized Burgers' equation
Non-linear kinematic wave for debris flow can be written as a generalized Burgers' equation with complex non-linear coefficients:
where
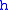 is the debris flow height,
is the debris flow height,  is the time,
is the time,  is the downstream channel position,
is the downstream channel position,  is the pressure gradient and the depth dependent nonlinear variable
is the pressure gradient and the depth dependent nonlinear variablewave speed, and
 is a flow height and pressure gradient dependent variable diffusion term.
is a flow height and pressure gradient dependent variable diffusion term.This equation can also be written in the conservative form:
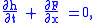
where
 is the generalized flux that depends on several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient. For
is the generalized flux that depends on several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient. For 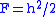 , this equation reduces to the Burgers' equation.
, this equation reduces to the Burgers' equation.External links
- Burgers' Equation at EqWorld: The World of Mathematical Equations.
- Burgers' Equation at NEQwiki, the nonlinear equations encyclopedia.
- Burgers shock-waves and sound in a 2D microfluidic droplets ensemble Phys. Rev. Lett. 103, 114502 (2009).

