Burmester's theory
Encyclopedia
Burmester's theory is named after Ludwig Burmester
(1840-1927). Burmester introduced geometric techniques for synthesis of linkages
in the late 19th century. His approach was to compute the geometric constraints of the linkage directly from the inventor's desired movement for a floating link. From this point of view a four-bar linkage is a floating link that has two points constrained to lie on two circles.
Burmester began with a set of locations, often called poses, for the floating link, which are viewed as snapshots of the constrained movement of this floating link in the device that is to be designed. The design of a crank
for the linkage now becomes finding a point in the moving floating link that when viewed in each of these specified positions has a trajectory that lies on a circle. The dimension of the crank is the distance from the point in the floating link, called the circling point, to the center of the circle it travels on, called the center point. Two cranks designed in this way form the desired four-bar linkage.
This formulation of the mathematical synthesis of a four-bar linkage and the solution to the resulting equations is known as Burmester Theory.
The approach has been generalized to the synthesis of spherical and spatial mechanisms.
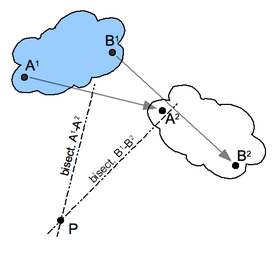Two positions: As an example consider a task defined by two positions of the coupler link, as shown in the figure. Choose two points A and B in the body, so its two positions define the segments A¹B¹ and A²B². It is easy to see that A is a circling point with a center that is on the perpendicular bisector of the segment A¹A². Similarly, B is a circling point with a center that is any point on the perpendicular bisector of B¹B². A four-bar linkage can be constructed from any point on the two perpendicular bisectors as the fixed pivots and A and B as the moving pivots. The point P is clearly special, because it is a hinge that allows pure rotational movement of A¹B¹ to A²B². It is called the relative displacement pole.
Three positions: If the designer specifies three task positions, then points A and B in the moving body are circling points each with a unique center point. The center point for A is the center of the circle that passes through A¹, A² and A³ in the three positions. Similarly, the center point for B is the center of the circle that passes through B¹, B² and B³. Thus for three task positions, a four-bar linkage is obtained for every pair of points A and B chosen as moving pivots.
Four positions: Graphical solution to the synthesis problem becomes more interesting in the case of four task positions, because not every point in the body is a circling point. Four task positions yield six relative displacement poles, and Burmester selected four to form the opposite pole quadrilateral, which he then used to graphically generate the circling point curve (Kreispunktcurven). Burmester also showed that the circling point curve was a circular cubic curve in the moving body.
Five positions: To reach five task positions, Burmester intersects the circling point curve generated by the opposite pole quadrilateral for a set of four of the five task positions, with the circling point curve generated by the opposite pole quadrilateral for different set of four task positions. Five poses imply ten relative displacement poles, which yields four different opposite pole quadrilaterals each having its own circling point curve. Burmester shows that these curves will intersect in as many as four points, called the Burmester points, each of which will trace five points on a circle around a center point. Because, two circling points define a four-bar linkage, these four points can yield as many as six four-bar linkages that guide the coupler link through the five specified task positions.
Ludwig Burmester
Ludwig Ernst Hans Burmester was a German kinematician and geometer.His doctoral thesis Über die Elemente einer Theorie der Isophoten concerned lines on a surface defined by light direction...
(1840-1927). Burmester introduced geometric techniques for synthesis of linkages
Linkage (mechanical)
A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...
in the late 19th century. His approach was to compute the geometric constraints of the linkage directly from the inventor's desired movement for a floating link. From this point of view a four-bar linkage is a floating link that has two points constrained to lie on two circles.
Burmester began with a set of locations, often called poses, for the floating link, which are viewed as snapshots of the constrained movement of this floating link in the device that is to be designed. The design of a crank
Crank
-Mechanism:* Crank , in mechanical engineering, a bent portion of an axle, or shaft, or an arm keyed at right angles to the end of a shaft, by which motion is imparted to or received from it...
for the linkage now becomes finding a point in the moving floating link that when viewed in each of these specified positions has a trajectory that lies on a circle. The dimension of the crank is the distance from the point in the floating link, called the circling point, to the center of the circle it travels on, called the center point. Two cranks designed in this way form the desired four-bar linkage.
This formulation of the mathematical synthesis of a four-bar linkage and the solution to the resulting equations is known as Burmester Theory.
The approach has been generalized to the synthesis of spherical and spatial mechanisms.
Finite position synthesis
Burmester theory seeks points in a moving body that have trajectories that lie on a circle called circling points. The designer approximates the desired movement with a finite number of task positions; and Burmester showed that circling points exist for as many as five task positions. Finding these circling points requires solving five quadratic equations in five unknowns, which he did using techniques in descriptive geometry. Burmester's graphical constructions still appear in machine theory textbooks to this day.Three positions: If the designer specifies three task positions, then points A and B in the moving body are circling points each with a unique center point. The center point for A is the center of the circle that passes through A¹, A² and A³ in the three positions. Similarly, the center point for B is the center of the circle that passes through B¹, B² and B³. Thus for three task positions, a four-bar linkage is obtained for every pair of points A and B chosen as moving pivots.
Four positions: Graphical solution to the synthesis problem becomes more interesting in the case of four task positions, because not every point in the body is a circling point. Four task positions yield six relative displacement poles, and Burmester selected four to form the opposite pole quadrilateral, which he then used to graphically generate the circling point curve (Kreispunktcurven). Burmester also showed that the circling point curve was a circular cubic curve in the moving body.
Five positions: To reach five task positions, Burmester intersects the circling point curve generated by the opposite pole quadrilateral for a set of four of the five task positions, with the circling point curve generated by the opposite pole quadrilateral for different set of four task positions. Five poses imply ten relative displacement poles, which yields four different opposite pole quadrilaterals each having its own circling point curve. Burmester shows that these curves will intersect in as many as four points, called the Burmester points, each of which will trace five points on a circle around a center point. Because, two circling points define a four-bar linkage, these four points can yield as many as six four-bar linkages that guide the coupler link through the five specified task positions.
See also
- Mechanical systemMechanical systemA mechanical system manages power to accomplish a task that involves forces and movement. Mechanical is derived from the Latin word machina, which in turn derives from the Doric Greek μαχανά , Ionic Greek μηχανή "contrivance, machine, engine" and that from μῆχος , "means, expedient, remedy".The...
- Machine (mechanical)Machine (mechanical)The mechanical properties of a machine manage power to achieve desired forces and movement. Modern machines often include computers and sensors that monitor performance and plan movement, and are called mechanical systems....
- Linkage (mechanical)Linkage (mechanical)A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...
- Klann linkageKlann LinkageThe Klann linkage is a planar mechanism designed to simulate the gait of legged animal and function as a wheel replacement. The linkage consists of the frame, a crank, two grounded rockers, and two couplers all connected by pivot joints....
Further reading
- Ian R. PorteousIan R. PorteousIan Robertson Porteous was a Scottish mathematician at the University of Liverpool and an educator on Merseyside. He is best known for three books on geometry and modern algebra...
(2001) Geometric Differentiation, § 3.5 Burmester Points, page 58, Cambridge University PressCambridge University PressCambridge University Press is the publishing business of the University of Cambridge. Granted letters patent by Henry VIII in 1534, it is the world's oldest publishing house, and the second largest university press in the world...
ISBN 0-521-00264-8 . - M. Ceccarelli and T. Koetsier, Burmester and Allievi: A Theory and Its Application for Mechanism Design at the End of the 19th Century, ASME 2006
External links
- R. E. Kaufman provides links to videos of KINSYN which is the original interactive graphics software implementing Burmester's four position synthesis.
- The University of Minnesota Lincages software implements Burmester's four position synthesis.
- The Synthetica 3.0 software applies Burmester's approach to the synthesis of spatial linkages.
- Linkage synthesis on mechanicaldesign101.com provides a Mathematica notebook for Burmester's five position synthesis.